强连通分量

Nannan Lv5
  2023-07-28 18:06 2023-07-28 18:06 Created   2024-09-30 19:44:28 2024-09-30 19:44:28 Updated      

强连通分量

一、强连通分量

1.DFS森林和强连通分

(1)DFS Forest

  • Tree Edge指树边
  • Back Edge指连向祖先的边(返祖边)
  • Forward Edge指连向子孙的边(前向边，它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点 并不是 当前结点的祖先。)
  • Cross Edge指连向树其他分支的边(横插边,它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点 并不是 当前结点的祖先。)
  • 在无向图只存在Tree Edge和Back Edge

![image-20230726153119895](C:\Users\Zhou Yanan\AppData\Roaming\Typora\typora-user-images\image-20230726153119895.png)

(2)强连通分量SCC(Strongly Connected Component)

![image-20230726154326777](C:\Users\Zhou Yanan\AppData\Roaming\Typora\typora-user-images\image-20230726154326777.png)

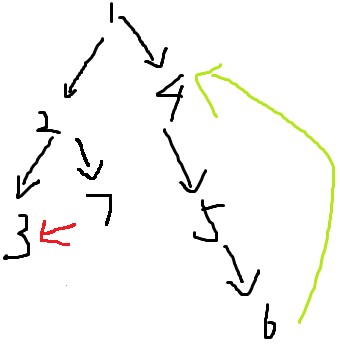
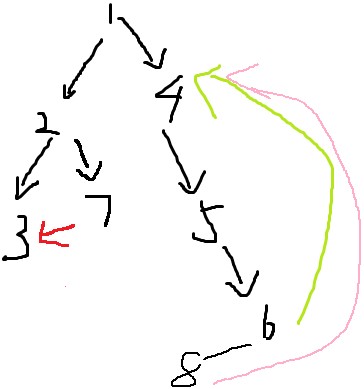
强连通：u存在到达v的路径，v存在到达u的路径，我们称u、v是强连通的（如图中绿框里面的）

推论：强连通强连通 ==> 强连通

2.SCC的Tarjan和Kosaraju算法

(1)Tarjan 算法求强连通分量

我们考虑把它切成一块一块的强连通分类，能切就切

![image-20230726154326777](C:\Users\Zhou Yanan\AppData\Roaming\Typora\typora-user-images\image-20230726154326777.png)

能切：

  • 不能连上去
  • 不能连向前面未切的点

接下来总结一下过程：

tarjan的过程就是dfs的过程。

遍历所有未被遍历的点，会得到一棵有向树，显然有向树没有环(注意搜过的点不会再搜)。所以能产生环的只有【指向已经遍历过的点】的边。

img

如图，环只可能由红色或绿色的边产生。

结论：红边不产生环，绿边产生环。

1、对于红边，连接的两个点3、7没有父子关系，这种边称为横叉边。

横叉边一定不产生环。

2、对于绿边，连接的两个点6、4是父子关系，这种边称为后向边。

环一定由后向边产生。

3、图中除了黑色的树枝边，一定只有横叉边和后向边（不存在其他种类的边）

来体会一下：

img

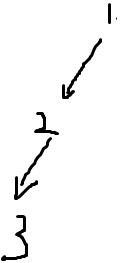
stk = {1，2，3},3没有多余的边，没得往下搜了，也没得往回返，那么3出栈，{3}作为一个强连通分量。

再次dfs

img

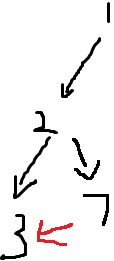
此时栈里是stk = {1.2.7}

我们发现红边7->3，3已经被遍历过，而3不在栈里面->3和7无父子关系->改边为横插边，我们无视它。

然后7出栈，形成强连通分量{7},2出栈，形成强连通分量{2}。

再次dfs

img

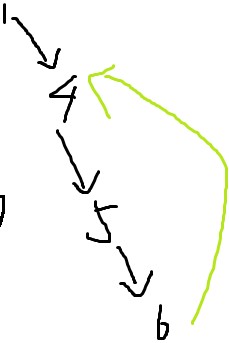
此时栈里面stk = {1,4,5,6}

我们发现了绿边指向了已经遍历过的点4->4在栈里面->4和6有父子关系->改边为返祖边

那么6，5，4出栈，{4，5，6}作为一个强连通分量。

然而情况可能更为复杂，出现大环套小环情况：

img

显然我们认为大环{4,5,6,8}是一个强连通分量。那么我们就需要low数组的帮忙。low[u] 表示 以u点为父节点的 子树 能连接到 [栈中] 最上端的点 的DFN值(换句话说，是最小的DFN，因为最上端的DFN是最小的嘛）

对于每个结点我们需要维护：

  1. :遍历时候结点被搜到的次序,本质上是一个时间戳。

  2. ：在的子树中能回溯到的最早的已经在栈中的结点。设以为根的子树为。 定义为以下结点的的最小值：中的结点；从通过一条不在搜索树上的边能到达的结点。简单的来说就是：是来记录每个顶点在不经过父顶点时，能够回到的最小“时间戳”。

    注意❗：其实我们不用那么严格确定的定义，它只用表达出现在这个点还能不能往上跳就行了。

    一个结点的子树内结点的 都大于该结点的 。

每当找到一个强连通元素，就按照该元素包含结点数目让栈中元素出栈。

在搜索过程中，对于结点和与其相邻的结点(不是的父节点)考虑 3 种情况：

  1. 未被访问：继续对进行深度搜索。在回溯过程中，用更新。因为存在从到 的直接路径，所以能够回溯到的已经在栈中的结点,也一定能够回溯到。
  2. 被访问过，已经在栈中：根据 low 值的定义，用更新。
  3. 被访问过，已不在栈中：说明已搜索完毕，其所在连通分量已被处理，所以不用对其做操作。

以上部分引用自：强连通分量及缩点tarjan算法解析 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N = 101000;
vector<int>edge[N];
int n,m;
int dfn[N],low[N],ins[N],idx,bel[N],cnt;
//         low记这个子树里面能跳到的dfn最小的，且未被切掉的(ins[u] = true)
stack<int>stk;
vector<vector<int>>scc;
void dfs(int u)
{
	dfn[u] = low[u] = ++idx;
	ins[u] = true;
	stk.push(u);//还没被切掉的点
	for(auto v:edge[u])
	{
		// if(!dfn[v]){
		// 	dfs(v);
		// 	low[u] = min(low[u],low[v]);
		// }
		// else{
		// 	if(ins[v])low[u] = min(low[u],dfn[v]);
		// }
		if(!dfn[v])dfs(v);
		if(ins[v])low[u] = min(low[u],low[v]);//这里可以乱搞写法，因为只要还能苟住就行，不一定一定记录最小的low
	}
	if(dfn[u] == low[u]){
		vector<int>c;
		++cnt;
		while(1)
		{
			int v = stk.top();
			c.push_back(v);
			ins[v] = false;
			bel[v] = cnt;
			stk.pop();
			if(u==v)break;
		}
		sort(c.begin(), c.end());
		scc.push_back(c);
	}

}

int main()
{
	cin>>n>>m;
	for(int i = 1;i<=m;i++)
	{
		int u,v;
		cin>>u>>v;
		edge[u].push_back(v);
	}

	for(int i = 1;i<=n;i++)
	{
		if(!dfn[i])dfs(i);
	}
	sort(scc.begin(),scc.end());
	for(auto c:scc)
	{
		for(auto u:c)
		{
			cout<<u<<" ";
		}
		cout<<"\n";
	}
}

(2)Kosaraju 算法

依靠2次DFS实现：

先DFS一遍：在回溯时候给出点编号，得到出栈顺序(即后序遍历)。

第二次DFS：对反图dfs,这样遍历到的所有点的集合就是一个强连通分量。

❗重要的几个结论

  1. DAG(有向无环图)出栈顺序是反图的拓扑序
  2. 有向图 SCC缩点(不考虑强连通分量内部的连边，只考虑强连通分量与强连通分量之间的连边)之后就是一个DAG
  3. 最后一个出栈的一定是源点(入度为0的点)
  4. Tarjan的SCC的点的编号是反向的拓扑序

![image-20230726154326777](C:\Users\Zhou Yanan\AppData\Roaming\Typora\typora-user-images\image-20230726154326777.png)

反着搜：6 2 3 9 7 4 14 12 13 10 15 11 5 1 0 8

![image-20230726165403338](C:\Users\Zhou Yanan\AppData\Roaming\Typora\typora-user-images\image-20230726165403338.png)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N = 101000;
vector<int>edge[N],erev[N];
vector<int>c,out;
int n,m;
bool vis[N];
vector<vector<int>>scc;
void dfs(int u)
{
	vis[u] = true;
	for(auto v:edge[u])
	{
		if(!vis[v])dfs(v);
	}
	out.push_back(u);
}


void dfs2(int u)
{
	vis[u] = true;
	for(auto v:erev[u])
	{
		if(!vis[v])dfs2(v);
	}
	c.push_back(u);
}


int main()
{
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i = 1;i<=m;i++)
	{
		int u,v;
		cin>>u>>v;
		edge[u].push_back(v);
		erev[v].push_back(u);
	}

	for(int i = 1;i<=n;i++)
	{
		if(!vis[i])dfs(i);
	}
	reverse(out.begin(),out.end());
	memset(vis,false,sizeof(vis));
	for(auto u: out)
	{
		if(!vis[u])
		{
			c.clear();
			dfs2(u);
			sort(c.begin(),c.end());
			scc.push_back(c);
		}
	}
	sort(scc.begin(),scc.end());
	for(auto c:scc)
	{
		for(auto u:c)
		{
			cout<<u<<" ";
		}
		cout<<endl;
	}
		
}

(3)例题：HAOI2006, 受欢迎的牛

看有多少点，所有点都可达

  • 对于DAG来说，唯一汇点是所有点都可达
  • 对于一般图来说，它SCC缩点之后是一个DAG，那么它要所有点都可达它，它必须是缩完点之后的唯一汇点。之后再去看SCC里面有多少个点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
//有多少个点，所有点都可达
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N = 101000;
vector<int>edge[N];
int n,m;
int dfn[N],low[N],ins[N],idx,bel[N],cnt,sz[N];//sz：每个强连通分量的size
//         low记这个子树里面能跳到的dfn最小的，且未被切掉的(ins[u] = true)
int outd[N];//每个强连通分量它的出度
stack<int>stk;
void dfs(int u)
{
	dfn[u] = low[u] = ++idx;
	ins[u] = true;
	stk.push(u);//还没被切掉的点
	for(auto v:edge[u])
	{
		if(!dfn[v])dfs(v);
		if(ins[v])low[u] = min(low[u],low[v]);
	}
	if(dfn[u] == low[u]){
		++cnt;
		while(1)
		{
			int v = stk.top();
			ins[v] = false;
			bel[v] = cnt;
			sz[cnt]++;
			stk.pop();
			if(u==v)break;
		}
	}

}

int main()
{
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	
	cin>>n>>m;
	for(int i = 1;i<=m;i++)
	{
		int u,v;
		cin>>u>>v;
		edge[u].push_back(v);
	}

	for(int i = 1;i<=n;i++)
	{
		if(!dfn[i])dfs(i);
	}
	for(int u = 1;u<=n;u++)
	{
		for(auto v : edge[u])
		{
			if(bel[u] != bel[v])
				outd[bel[u]]++;
		}
	}

	int cnts = 0,cntv = 0;
	for(int i = 1;i<=cnt;i++)
	{
		if(outd[i]==0)
		{
			cnts++;
			cntv += sz[i];
		}
	}
	if(cnts>=2)//有两个汇点，这两个汇点之间是不可达的
		cout<<0<<"\n";
	else
		cout<<cntv<<"\n";
}

3.SCC缩点和DP

考虑：什么时候要用缩点？

我们知道，对于DAG来说，因为木有环，所以我们可以快乐的在上面跑dfs，跑dp。因为如果有环，它就会在上面转圈圈跑啊跑啊跑，很好，这就得到了TLE的结果了，如果用vis标记，虽然不T了，但是你不能保证结果最优。

那么当你发现，这个题目显然满足贪心，这个环每个点的最大贡献都是整个环的总贡献，那么这个时候缩点就很有必要了。把这个环的点缩成一个点，那么这个点的贡献就代表了这个环的贡献。

上述中的环可以理解为强连通分量，因为我们缩点完之后可能还是有环的。

如何缩点？

把同一个强连通分量中的点权加起来，当成一个点，这些点的点权和就是这个点的点权，完成缩点。

以下是一些例题…QAQ

例题1：ZJOI2007, 最大半连通子图

思路：

对于DAG来说，我们找最大半连通子图就是找一条最长路。

那么对于一般图，我们考虑缩点。缩点之后转化为带权的求最长路问题。

步骤：

  1. SCC缩点
  2. DP
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N = 101000;
vector<int>edge[N];
int n,m,cnt,mod;;
int dfn[N],low[N],ins[N],idx,bel[N];
//         low记这个子树里面能跳到的dfn最小的，且未被切掉的(ins[u] = true)
stack<int>stk;
vector<int>vec[N];
int dp[N],way[N];
bool vis[N];
void dfs(int u)
{
	dfn[u] = low[u] = ++idx;
	ins[u] = true;
	stk.push(u);//还没被切掉的点
	for(auto v:edge[u])
	{
		if(!dfn[v])dfs(v);
		if(ins[v])low[u] = min(low[u],low[v]);
	}
	if(dfn[u] == low[u]){
		++cnt;
		while(1)
		{
			int v = stk.top();
			vec[cnt].push_back(v);//记录每个强连通分量有哪些点
			ins[v] = false;
			bel[v] = cnt;
			stk.pop();
			if(u==v)break;
		}
	}
}

int main()
{
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);

	cin>>n>>m>>mod;
	for(int i = 1;i<=m;i++)
	{
		int u,v;
		cin>>u>>v;
		edge[u].push_back(v);
	}

	for(int i = 1;i<=n;i++)
		if(!dfn[i])dfs(i);

	int ans = 0,w = 0;
	for(int i = 1;i<=cnt;i++)
	{
		way[i] = 1;
		dp[i] = 0;
		for(int u : vec[i])
		{
			for(int v :edge[u])
			{
				if(!vis[bel[v]]&&bel[v]!=i)	//注意缩完点之后连边注意重边不要重复计算
				{
					vis[bel[v]] = true;
					if(dp[bel[v]]>dp[i])
						dp[i] = dp[bel[v]],way[i] = 0;
					if(dp[bel[v]]==dp[i])
						way[i] = (way[i]+way[bel[v]])%mod;
				}
			}
		}
		dp[i] += vec[i].size();
		if(dp[i]>ans)
			ans = dp[i],w = 0;
		if(dp[i]==ans)
			w = (w+way[i])%mod;
		for(int u : vec[i])
			for(int v :edge[u])
				vis[bel[v]] = false;

	}
	cout<<ans<<"\n";
	cout<<w<<"\n";

}

写法2：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N = 101000;
vector<int>edge[N];
int n,m,mod;
int cnt,idx;
int dfn[N],low[N],ins[N],bel[N];
int dp[N],vis[N],way[N];
int ans,w,T;
stack<int>stk;


void dfs(int u)
{
	dfn[u] = low[u] = ++idx;
	ins[u] = true;
	stk.push(u);

	for(auto v:edge[u])
	{
		if(!dfn[v])dfs(v);
		if(ins[v])low[u] = min(low[u],low[v]);
	}
	if(dfn[u]==low[u])
	{
		++cnt;
		int sz = 0;
		dp[cnt] = 0;
		way[cnt] = 1;
		++T;
		vis[cnt] = T;
		while(1)
		{
			int v = stk.top();
			stk.pop();
			ins[v] = false;
			bel[v] = cnt;
			sz++;
			for(auto w:edge[v])
			{
				if(vis[bel[w]]!=T&&bel[w]!=0)
				{
					vis[bel[w]] = T;
					if(dp[bel[w]]>dp[cnt])
						dp[cnt] = dp[bel[w]],way[cnt] = way[bel[w]];
					else if(dp[bel[w]]==dp[cnt])
						way[cnt] = (way[cnt]+way[bel[w]])%mod;
				}
			}
			if(u==v)break;
		}
		dp[cnt] += sz;
		if(dp[cnt]>ans)
			ans = dp[cnt],w = way[cnt];
		else if(dp[cnt]==ans)
			w = (w+way[cnt])%mod;
	}
}


void tarjan()
{
	for(int i = 1;i<=n;i++)
		if(!dfn[i])dfs(i);
}


int main()
{
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>n>>m>>mod;
	for(int i = 1;i<=m;i++)
	{
		int u,v;
		cin>>u>>v;
		edge[u].push_back(v);
	}
	tarjan();
	cout<<ans<<"\n";
	cout<<w<<"\n";
	return 0;
}

例题2：APIO2009, ATM 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N = 501000;
vector<int>edge[N];
int n,m;
int dfn[N],low[N],ins[N],idx,bel[N],cnt;
//         low记这个子树里面能跳到的dfn最小的，且未被切掉的(ins[u] = true)
stack<int>stk;
int val[N],bar[N];
ll dp[N];
void dfs(int u)
{
	dfn[u] = low[u] = ++idx;
	ins[u] = true;
	stk.push(u);//还没被切掉的点
	for(auto v:edge[u])
	{
		if(!dfn[v])dfs(v);
		if(ins[v])low[u] = min(low[u],low[v]);
	}
	if(dfn[u] == low[u]){
		++cnt;
		ll sval = 0;
		bool sbar = false;
		dp[cnt] = -(1ll<<60);
		while(1)
		{
			int v = stk.top();
			stk.pop();
			ins[v] = false;
			bel[v] = cnt;
			sval += val[v];
			sbar |= bar[v];
			for(auto w:edge[v])
			{
				if(bel[w]!= cnt && bel[w] != 0)
				{
					dp[cnt] = max(dp[cnt],dp[bel[w]]);
				}
			}
			if(u==v)break;
		}
		if(sbar)dp[cnt] = max(dp[cnt],0ll);
		dp[cnt] += sval;
	}
}
int main()
{
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);

	cin>>n>>m;
	for(int i = 1;i<=m;i++)
	{
		int u,v;
		cin>>u>>v;
		edge[u].push_back(v);
	}
	for(int i = 1;i<=n;i++)
		cin>>val[i];
	int s,p;
	cin>>s>>p;
	for(int i = 1;i<=p;i++)
	{
		int x;
		cin>>x;
		bar[x] = 1;
	}
	dfs(s);
	cout<<dp[bel[s]]<<"\n";
}

例题3：SDOI2010, 所驼门王的宝藏

思路：首先思考一下怎么去建图？

一共有个点，如果所有的可达信息都建出来，这复杂度太高了。

那怎么办呢？考虑建立辅助结点。

比如有一个横向的传送门，它可以到这一行所有的点。那么我们考虑先建立一个辅助点，这个辅助点向这一行所有点连边，再把这个有横向传送门的点连向辅助点。这样就可以实现，该点先到辅助点，辅助点再到所有点。

注意点：

  1. 统计size的时候注意不要把辅助点加进去了。
  2. 记录编号数组稍微开大一点(至少开两倍)，因为我们还要记录辅助点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N = 301000;
vector<int>edge[N];

map<int,vector<int>>r,c;
map<int,int>rid,cid;
map<pair<int,int>,int>id;

int dfn[N],low[N],ins[N],idx,bel[N],cnt;
stack<int>stk;
int n,R,C,dp[N],ans,x[N],y[N],ty[N];

int tot;
void dfs(int u)
{
	dfn[u] = low[u] = ++idx;
	ins[u] = true;
	stk.push(u);//还没被切掉的点
	for(auto v:edge[u])
	{
		if(!dfn[v])dfs(v);
		if(ins[v])low[u] = min(low[u],low[v]);
	}
	if(dfn[u] == low[u]){
		++cnt;
		int sz = 0;
		dp[cnt] = 0;
		while(1)
		{
			int v = stk.top();
			ins[v] = false;
			bel[v] = cnt;
			sz+=(v<=n);
			stk.pop();
			for(auto w:edge[v])
			{
				if(bel[w]!=cnt&&bel[w]!=0)
				{
					dp[cnt] = max(dp[cnt],dp[bel[w]]);
				}		
			}
			if(u==v)break;
		}
		dp[cnt] += sz;
		ans  = max(ans,dp[cnt]);
	}
}
void tarjan()
{
	for(int i = 1;i<=tot;i++)
	{
		if(!dfn[i])dfs(i);
	}
}


int main()
{
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);

	cin>>n>>R>>C;
	for(int i = 1;i<=n;i++)
	{
		cin>>x[i]>>y[i]>>ty[i];
		id[{x[i],y[i]}] = i;
		r[x[i]].push_back(i);
		c[y[i]].push_back(i);
	}
	tot = n;
	for(int i  = 1;i<=n;i++)
	{
		if(ty[i]==1)
		{
			if(!rid.count(x[i]))
			{
				rid[x[i]] = ++tot;
				for(auto id:r[x[i]])edge[tot].push_back(id);
			}
			edge[i].push_back(rid[x[i]]);
		}
		else if(ty[i]==2)
		{
			if(!cid.count(y[i]))
			{
				cid[y[i]] = ++tot;
				for(auto id:c[y[i]])edge[tot].push_back(id);
			}
			edge[i].push_back(cid[y[i]]);
		}
		else if(ty[i]==3)
		{
			for(int dx = -1;dx<=1;dx++)
			{
				for(int dy = -1;dy<=1;dy++)
				{
					if(dx==0&&dy==0)continue;
					if(!id.count({x[i]+dx,y[i]+dy}))continue;
					edge[i].push_back(id[{x[i]+dx,y[i]+dy}]);
				}
			}

		}
	}
	tarjan();
	cout<<ans<<"\n";
}
  • Title: 强连通分量
  • Author: Nannan
  • Created at : 2023-07-28 18:06:00
  • Updated at : 2024-09-30 19:44:28
  • Link: https://redefine.ohevan.com/2023/07/28/四、强连通分量/
  • License: This work is licensed under CC BY-NC-SA 4.0.
Comments
On this page
强连通分量
  1. 强连通分量
    1. 一、强连通分量
      1. 1.DFS森林和强连通分
        1. (1)DFS Forest
        2. (2)强连通分量SCC(Strongly Connected Component)
      2. 2.SCC的Tarjan和Kosaraju算法
        1. (1)Tarjan 算法求强连通分量
        2. (2)Kosaraju 算法
      3. ❗重要的几个结论
        1. (3)例题：HAOI2006, 受欢迎的牛
      4. 3.SCC缩点和DP
        1. 例题1：ZJOI2007, 最大半连通子图
        2. 例题2：APIO2009, ATM
        3. 例题3：SDOI2010, 所驼门王的宝藏