树链剖分

Nannan Lv5
  2023-11-25 16:47 2023-11-25 16:47 Created   2024-09-30 19:49:28 2024-09-30 19:49:28 Updated      

树链剖分

一、树链剖分的概念和写法

1.1概念

定义：树链剖分用于将树分割成若干条链的形式，以维护树上路径的信息。具体来说，将整棵树剖分为若干条链，使它组合成线性结构，然后用其他的数据结构维护信息。

树链剖分（树剖/链剖）有多种形式，如 重链剖分，长链剖分 和用于 Link/cut Tree 的剖分（有时被称作「实链剖分」），大多数情况下（没有特别说明时），「树链剖分」都指「重链剖分」。

树链剖分一般可以做：路径修改\查询，子树修改\查询

一些定义：

定义 重儿子节点 表示其子节点中子树最大的子结点。如果有多个子树最大的子结点，取其一。如果没有子节点，就无重子节点。

定义 轻儿子节点 表示剩余的所有子结点。

从这个结点到重子节点的边为 重边。

到其他轻子节点的边为 轻边。

若干条首尾衔接的重边构成 重链。

把落单的结点也当作重链，那么整棵树就被剖分成若干条重链。

树链剖分

我们观察图中，重链是以轻儿子或整棵树的根为起点，依次向下连接所有重儿子组成的链。而轻链是以重链为主干链，其分支的链为轻链的，且向外扩展长度为1。

轻链的本质就是一些长度为1的边，将他们作为桥梁连接下一个重链。同时还可以看出，轻儿子(除去叶子结点)都是下一条重链的起始结点。

两遍dfs就是树链剖分的主要处理，通过dfs我们已经保证一条重链上各个节点dfs序连续，那么可以想到，我们可以通过数据结构（以线段树为例）来维护一条重链的信息

第一遍处理每个点的重儿子,节点大小，深度,每个点的父亲

第二遍，求出每个点的序，重链上的链头的元素。

❗关于第二遍：

首先根据，先所有的重链，遍历重链过程中，传递下去值；再以重链为主干，遍历所有的轻链，因为轻结点会是重链的起点，因此，又可以得到新的重链，依次下去。同时先重链，保证了重链的序的连续的,即不仅在子树里面dfs序是连续的，在重链里面也是连续的。

HLD

为什么要记录链头元素？(该部分引用自 )

我们得到了一系列的重链，如何对它们快速操作？那么就是记录链头元素。这样我们就可以直接跳到链头元素。但是我们遇到了一个问题：在同一条重链上可以直接跳到头部，如果不是在同一条链上呢？方法是：从这条重链的头部再往上跳，到他的父亲结点，必定在另外一条重链上，然后根据需求继续跳。如图所示，b结点跳跃的过程：

b结点跳跃示意图

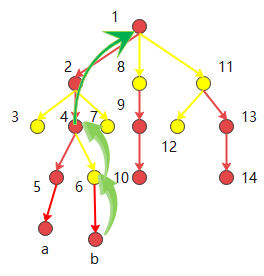
b在{6 b}这条重链，跳至6号结点，从6号再跳到{1 2 4 5 a}这条重链，再跳就是1根节点。到这里，再想想什么是轻链，理解会更深刻“将他们作为“桥梁”连接下一个重链”。

1.2 (重要)性质

经过轻边，子树大小翻倍。一个点往上走，最多走条轻边。任意两点u，v，最多经过条。重链也是不超过段的。

1.3基本实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include<bits/stdc++.h>
using namespace std;

const int N = 1e5+10;
vector<int>e[N];
int l[N],r[N],id[N],sz[N],hs[N],tot,dep[N],f[N],top[N];
//第一遍dfs处理每个点的重儿子,节点大小，深度,每个点的父亲
void dfs1(int u,int fa)
{
	sz[u] = 1;
	hs[u] = -1;
	dep[u] = dep[fa]+1;
	f[u] = fa
	for(auto v:e[u])
	{
		if(v==fa)continue;
		dfs1(v,u);
		sz[u]+=sz[v];
		if(hs[u]==-1||sz[v]>sz[hs[u]])hs[u] = v;
	}
}

//第二步dfs，求出每个点的dfs序，重链上的链头的元素
void dfs2(int u,int t)//keep表示需不需要保留当前信息
{
	top[u] = t;
	l[u] = ++tot;
	id[tot] = u;

	if(hs[u]!=-1)
		dfs2(hs[u],t);//重儿子的集合
	for(auto v:e[u])
	{
		if(v!=fa[u]&&v!=hs[u])//v是轻儿子,它的链头就是它本身
		{
			dfs2(v,v);
		}
	}
	r[u] = tot;
}

int main()
{
	cin>>n;
	for(int i = 1;i<=n;i++)
	{
		int u,v;
		cin>>u>>v;
		e[u].push_back(v);
		e[v].push_back(u);
	}
	dfs1(1,0);
	dfs2(1,1);
	return 0;
}

1.4 简单应用：树链剖分求

预处理时间复杂度，查询时间复杂度

在这里插入图片描述

以上图为例，求的。

首先思考两个问题：

  1. 谁先跳？

    深度大的先跳。这时候你会想，那，的深度一样呀。不是的，不是直接比较，的深度，而是比较，向上跳一个链的深度。结点所在的重链往上跳一个链就是到号结点，而所在重链，往上跳也就是到了。我们需要比较的是号和号结点的深度，显然号深度更大，那么先跳。

  2. 什么时候能判断出？
    如果两个点在同一重链上，那么深度较小的，为，否则还是要不断的跳。、结点，当结点跳到结点时，和在同一重链中，即，所以为、最终的。

例题：树上LCA2 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include<bits/stdc++.h>
using namespace std;

const int N = 1e5+10;
vector<int>e[N];
int l[N],r[N],id[N],sz[N],hs[N],tot,dep[N],f[N],top[N];
int n,m;
//第一遍dfs处理每个点的重儿子,节点大小，深度,每个点的父亲
void dfs1(int u,int fa)
{
	sz[u] = 1;
	hs[u] = -1;
	dep[u] = dep[fa]+1;
	f[u] = fa;
	for(auto v:e[u])
	{
		if(v==fa)continue;
		dfs1(v,u);
		sz[u]+=sz[v];
		if(hs[u]==-1||sz[v]>sz[hs[u]])hs[u] = v;
	}
}

//第二步dfs，求出每个点的dfs序，重链上的链头的元素
void dfs2(int u,int t)//keep表示需不需要保留当前信息
{
	
	l[u] = ++tot;
	id[tot] = u;
	top[u] = t;
	if(hs[u]!=-1)
		dfs2(hs[u],t);//重儿子的集合
	for(auto v:e[u])
	{
		if(v!=f[u]&&v!=hs[u])//v是轻儿子,它的链头就是它本身
		{
			dfs2(v,v);
		}
	}
	r[u] = tot;
}

int LCA(int u,int v)
{
	while(top[u]!=top[v])
	{
		if(dep[top[u]]<dep[top[v]])v = f[top[v]];
		else u = f[top[u]];
	}
	if(dep[u]<dep[v])return u;
	else return v;
}


int main()
{
	cin>>n;
	for(int i = 1;i<n;i++)
	{
		int u,v;
		cin>>u>>v;
		e[u].push_back(v);
		e[v].push_back(u);
	}
	dfs1(1,0);
	dfs2(1,1);
	cin>>m;
	for(int i = 1;i<=m;i++)
	{
		int u,v;
		cin>>u>>v;
		cout<<LCA(u,v)<<"\n";	
	}
	return 0;
}

二、树链剖分的路径查询

根据上面第一点中所说的，在第二遍中，先重链，再轻链，这样保证了序不仅在子树中是连续的，在重链中也是连续的。

此时我们考虑对整个序建线段树。我们重链的一段，就是序的一段。

考虑一个点跳到，我们需要维护的就是到的信息，再让。即每跳一段就维护一段的信息。即在序中到这一段（就是序的编号）

![image-20230719124832251](C:\Users\Zhou Yanan\AppData\Roaming\Typora\typora-user-images\image-20230719124832251.png)

例题：SDOI2011, 染色

题意：

给定一棵个节点的无根树，共有 个操作，操作分为两种：

  1. 将节点 到节点 的路径上的所有点（包括 和）都染成颜色 。
  2. 询问节点 到节点 的路径上的颜色段数量。

颜色段的定义是极长的连续相同颜色被认为是一段。例如 112221 由三段组成：11、222、1。

思路：考虑从到的路径，那要考虑要两边一起跳。

注意点如下图：

![image-20230719180423336](C:\Users\Zhou Yanan\AppData\Roaming\Typora\typora-user-images\image-20230719180423336.png)序和我们实际路径可能是反着的，这个要注意！

![image-20230719180432224](C:\Users\Zhou Yanan\AppData\Roaming\Typora\typora-user-images\image-20230719180432224.png)注意拼接顺序❗

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5+10;
vector<int>e[N];
int l[N],r[N],idx[N],sz[N],hs[N],tot,dep[N],f[N],top[N],w[N];
int n,m;
struct info
{
    int lc,rc,seg;
};

info operator+(const info &l,const info &r)
{
    return (info){l.lc,r.rc,l.seg+r.seg+(l.rc!=r.lc)};
}

struct node{
    info val;
    int t;
}seg[N*4];


void settag(int id,int t)
{
    seg[id].val = {t,t,0};
    seg[id].t = t;
}

void pushdown(int id)
{
    if(seg[id].t!=0)
    {
        settag(id*2,seg[id].t);
        settag(id*2+1,seg[id].t);
        seg[id].t = 0;
    }
}
void update(int id)
{
    seg[id].val = seg[id*2].val+seg[id*2+1].val;
}

void build(int id,int l,int r)
{
    if(l==r)
    {
        //l号点，dfs序中第l个点,而不是a[l],这里要注意❗
        //seg[id].val = {a[l],a[l]};
        seg[id].val = {w[idx[l]],w[idx[l]],0};
    }
    else 
    {
        int mid = (l+r)>>1;
        build(id*2,l,mid);
        build(id*2+1,mid+1,r);
        update(id);
    }
}


void modify(int id,int l,int r,int x,int y,int t){
    if(l==x&&r==y)
    {
        settag(id,t);
        return;
    }
    int mid = (l+r)/2;
    pushdown(id);
    if(y<=mid) modify(id*2,l,mid,x,y,t);
    else if(x>mid) modify(id*2+1,mid+1,r,x,y,t);
    else{
        modify(id*2,l,mid,x,mid,t),modify(id*2+1,mid+1,r,mid+1,y,t);
    }
    update(id);
}

//O(logn)
info query(int id,int l,int r,int x,int y)
{
    if(l==x&&r==y)return seg[id].val; 
    int mid = (l+r)/2;
    pushdown(id);
    if(y<=mid)return query(id*2,l,mid,x,y);
    else if(x>mid)return query(id*2+1,mid+1,r,x,y);
    else{
        return query(id*2,l,mid,x,mid)+query(id*2+1,mid+1,r,mid+1,y);
    }

}

//第一遍dfs处理每个点的重儿子,节点大小，深度,每个点的父亲
void dfs1(int u,int fa)
{
    sz[u] = 1;
    hs[u] = -1;
    dep[u] = dep[fa]+1;
    f[u] = fa;
    for(auto v:e[u])
    {
        if(v==fa)continue;
        dfs1(v,u);
        sz[u]+=sz[v];
        if(hs[u]==-1||sz[v]>sz[hs[u]])hs[u] = v;
    }
}

//第二步dfs，求出每个点的dfs序，重链上的链头的元素
void dfs2(int u,int t)//keep表示需不需要保留当前信息
{
    
    l[u] = ++tot;
    idx[tot] = u;
    top[u] = t;
    if(hs[u]!=-1)
        dfs2(hs[u],t);//重儿子的集合
    for(auto v:e[u])
    {
        if(v!=f[u]&&v!=hs[u])//v是轻儿子,它的链头就是它本身
        {
            dfs2(v,v);
        }
    }
    r[u] = tot;
}

int LCA(int u,int v)
{
    while(top[u]!=top[v])
    {
        if(dep[top[u]]<dep[top[v]])v = f[top[v]];
        else u = f[top[u]];
    }
    if(dep[u]<dep[v])return u;
    else return v;
}


int query(int u,int v)
{
    info ansu = {0,0,-1},ansv={0,0,-1};
    while(top[u]!=top[v])
    {
        if(dep[top[u]]<dep[top[v]]){
            ansv = query(1,1,n,l[top[v]],l[v]) + ansv;//在前面加一段
            v = f[top[v]];
        }
        else{
            ansu = query(1,1,n,l[top[u]],l[u]) + ansu;
            u = f[top[u]];
        }
    }
    if(dep[u]<=dep[v])ansv = query(1,1,n,l[u],l[v])+ansv;
    else ansu = query(1,1,n,l[v],l[u])+ansu;
    return ansu.seg+ansv.seg+(ansu.lc!=ansv.lc)+1;
}

void modify(int u,int v,int c)
{
    // while(top[u]!=top[v])
    // {
    //     if(dep[top[u]]<dep[top[v]]){
    //        modify(1,1,n,l[top[v]],l[v],c);
    //        v = f[top[v]];
    //     }
    //     else{
    //         modify(1,1,n,l[top[u]],l[u],c);
    //         u = f[top[u]];
    //     }
    // }
    // if(dep[u]<=dep[v])modify(1,1,n,l[u],l[v],c);
    // else modify(1,1,n,l[v],l[u],c);

    while(top[u]!=top[v])
    {
        if(dep[top[u]]>dep[top[v]])swap(u,v);
        modify(1,1,n,l[top[v]],l[v],c);
        v = f[top[v]];
    }
    if(dep[u]>dep[v])swap(u,v);
    modify(1,1,n,l[u],l[v],c);
}

int main()
{
    cin>>n>>m;
    for(int i = 1;i<=n;i++)
        cin>>w[i];
    for(int i = 1;i<n;i++)
    {
        int u,v;
        cin>>u>>v;
        e[u].push_back(v);
        e[v].push_back(u);
    }


    dfs1(1,0);
    dfs2(1,1);
    build(1,1,n);
    for(int i = 1;i<=m;i++)
    {
        char op;
        cin>>op;
        if(op=='Q')
        {
            int u,v;
            cin>>u>>v;
            cout<<query(u,v)<<endl;
        }
        else
        {
            int u,v,c;
            cin>>u>>v>>c;
            modify(u,v,c);
        }
    }
    return 0;
}

三、树链剖分的子树查询

例题：NOI2015, 软件包管理器

题意：要下载某一个软件，就要把该软件到根路径上的所有没下载的软件都下载了。问每次操作完，有多少个软件包状态发生改变(从安装到没安装，或者从没安装到安装)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5+10;
vector<int>e[N];
int l[N],r[N],idx[N],sz[N],hs[N],tot,dep[N],f[N],top[N],w[N];
int n,m;

struct node{
    int cnt;
    int sz;
    int t;
}seg[N*4];


void settag(int id,int t)
{
    if(t==1)
        seg[id].cnt = seg[id].sz;
    else seg[id].cnt = 0;
    seg[id].t = t;
}

void pushdown(int id)
{
    if(seg[id].t!=-1)
    {
        settag(id*2,seg[id].t);
        settag(id*2+1,seg[id].t);
        seg[id].t = -1;
    }
}
void update(int id)
{
    seg[id].cnt= seg[id*2].cnt+seg[id*2+1].cnt;
}

void build(int id,int l,int r)
{
    seg[id].sz = (r-l+1);
    seg[id].t = -1;
    if(l==r)
    {
        seg[id].cnt = 0;
    }
    else 
    {
        int mid = (l+r)>>1;
        build(id*2,l,mid);
        build(id*2+1,mid+1,r);
        update(id);
    }
}


void modify(int id,int l,int r,int x,int y,int t){
    if(l==x&&r==y)
    {
        settag(id,t);
        return;
    }
    int mid = (l+r)/2;
    pushdown(id);
    if(y<=mid) modify(id*2,l,mid,x,y,t);
    else if(x>mid) modify(id*2+1,mid+1,r,x,y,t);
    else{
        modify(id*2,l,mid,x,mid,t),modify(id*2+1,mid+1,r,mid+1,y,t);
    }
    update(id);
}


//第一遍dfs处理每个点的重儿子,节点大小，深度,每个点的父亲
void dfs1(int u,int fa)
{
    sz[u] = 1;
    hs[u] = -1;
    dep[u] = dep[fa]+1;
    f[u] = fa;
    for(auto v:e[u])
    {
        if(v==fa)continue;
        dfs1(v,u);
        sz[u]+=sz[v];
        if(hs[u]==-1||sz[v]>sz[hs[u]])hs[u] = v;
    }
}

//第二步dfs，求出每个点的dfs序，重链上的链头的元素
void dfs2(int u,int t)//keep表示需不需要保留当前信息
{
    
    l[u] = ++tot;
    idx[tot] = u;
    top[u] = t;
    if(hs[u]!=-1)
        dfs2(hs[u],t);//重儿子的集合
    for(auto v:e[u])
    {
        if(v!=f[u]&&v!=hs[u])//v是轻儿子,它的链头就是它本身
        {
            dfs2(v,v);
        }
    }
    r[u] = tot;
}

void install(int x)
{
    while(x!=0)
    {
        modify(1,1,n,l[top[x]],l[x],1);
        x = f[top[x]];
    }
}




void uninstall(int x)
{
    modify(1,1,n,l[x],r[x],0);
}

int main()
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin>>n;
    for(int i = 2;i<=n;i++)
    {
         cin>>f[i];
         ++f[i];
         e[f[i]].push_back(i);
    }
    dfs1(1,0);
    dfs2(1,1);
    build(1,1,n);
    cin>>m;
    int pre = 0;
    for(int i = 1;i<=m;i++)
    {
        string op;
        int x;
        cin>>op>>x;
        x++;
        if(op=="install")
        {
            install(x);
        }
        else
        {
            uninstall(x);
        }
        cout<<abs(seg[1].cnt-pre)<<"\n";
        pre = seg[1].cnt;
    }
    return 0;
}

四、总结

树链剖分把路径问题转为为个区间问题。

  • Title: 树链剖分
  • Author: Nannan
  • Created at : 2023-11-25 16:47:00
  • Updated at : 2024-09-30 19:49:28
  • Link: https://redefine.ohevan.com/2023/11/25/八、树链剖分/
  • License: This work is licensed under CC BY-NC-SA 4.0.
Comments
On this page
树链剖分
  1. 树链剖分
    1. 一、树链剖分的概念和写法
      1. 1.1概念
      2. 1.2 (重要)性质
      3. 1.3基本实现
      4. 1.4 简单应用：树链剖分求
        1. 例题：树上LCA2
    2. 二、树链剖分的路径查询
      1. 例题：SDOI2011, 染色
    3. 三、树链剖分的子树查询
      1. 例题：NOI2015, 软件包管理器
    4. 四、总结