【从零开始的机器学习之旅】01-Regression

-Regression

Machine Learning ≈ Looking for Function

1.Different types of Functions

Regression:要找的函数,他的输出是一个数值

Classification:函数的输出，就说从设定好的选项里面，选择一个当作输出

Structured Learning:机器产生有结构的东西的问题——学会创造

---

2.A Case Study——预测频道的流量

2.1找到函数的三个步骤

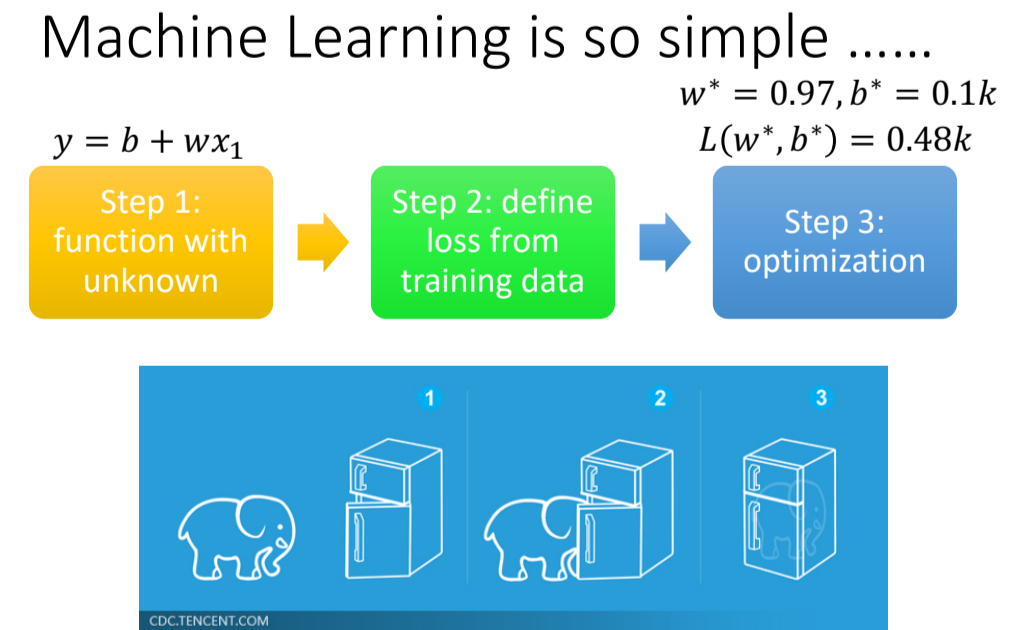
1. Function with Unknown Parameters(写出一个带有未知参数的函数) ⇒ Model

• 是我们准备要预测的东西(在这里就说频道的流量)
• 是这个频道前一天总观看人数
• 和是未知参数

猜测：未来的点阅次数的函数等于前一天点阅次数乘上再加上。(即)

⇒ 猜测往往就来自于对中国问题本质上的了解 ⇒ Domain knowledge

2. Define Loss from Training Data

​

​ Loss也是一个Function，它的输入是Model里面的参数。

这里：输入为:

• 物理意义：Loss Function输出的值代表——现在如果把当前这一组未知参数设定为某一组确定的数值的时候，这组数值的好坏程度。

  Loss 越大表示这一组参数越不好，反之越好。

• 计算方法：求取估测的值和实际的值(Label)之间的差距

  MAE(mean absolute error)

  MSE(mean square error)

  Cross-entropy:计算概率分布之间的差距

  Error Surface：试了不同的参数,然后计算它的Loss,画出来的这个等高线图

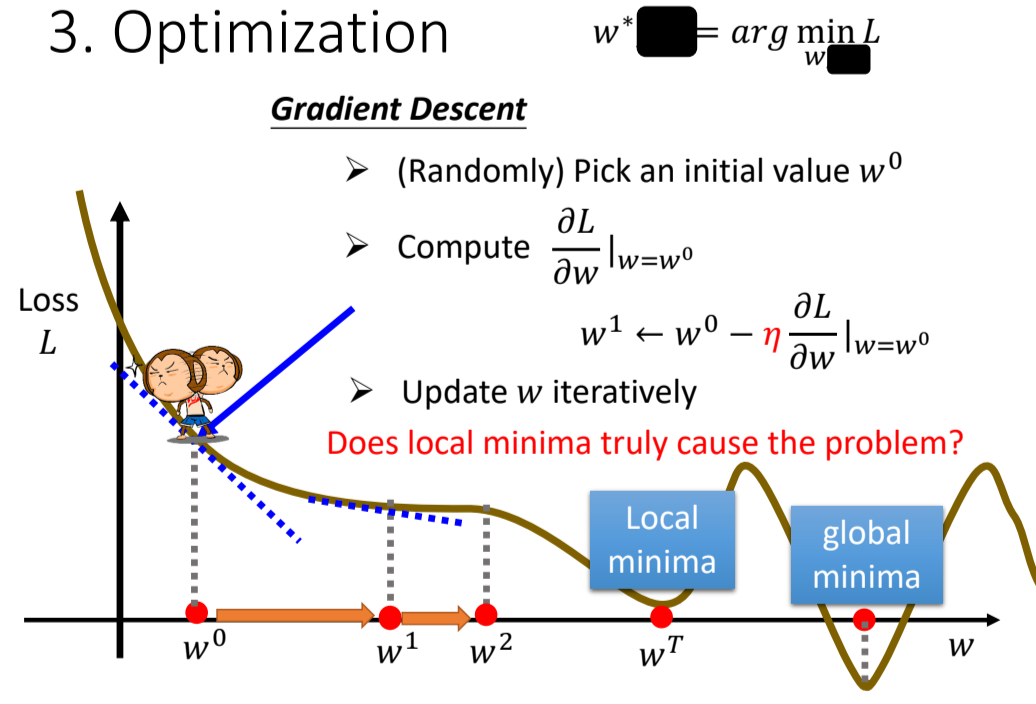
3. Optimization（优化）

找到能让损失函数值最小的参数。

具体方法：Gradient Descent（梯度下降）

先只考虑参数:

梯度下降步骤：

1. 随机选取初始值
2. 计算在的时候对的偏导代入的值(梯度)，即

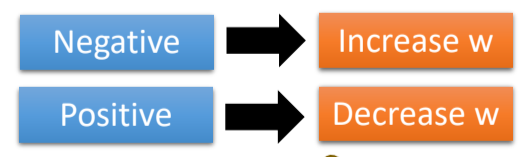
3. 根据微分(梯度)的方向，改变参数的值

​

​ 改变的大小取决于：

• 斜率大小
• 学习率(learning rate，超参数)

1. 什么时候停下来呢？

   a. 自己设置上限(超参数)

   b. 理想情况：微分值为0（极小值点），不会再更新⇒有可能陷入局部最小值，不能找到全局最小值

   事实上：局部最小值不是真正的问题！！！

   

​ 让我们推广到多个参数的情况(）：

​

---

3.Liner Model（线性模型）

根据周期性，修改模型⇒考虑前7天，甚至更多天的值

Model 的Bias：一个模型无法模拟/描述真实的情况

⇒解决方法：需要一个更复杂的、更有弹性的、有未知参数的function

4.⭐Piecewise Linear Curves（Sigmoid函数的意义）

4.1.模型定义

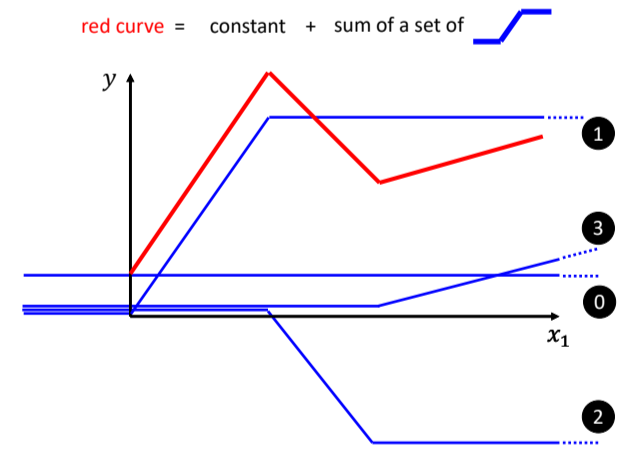
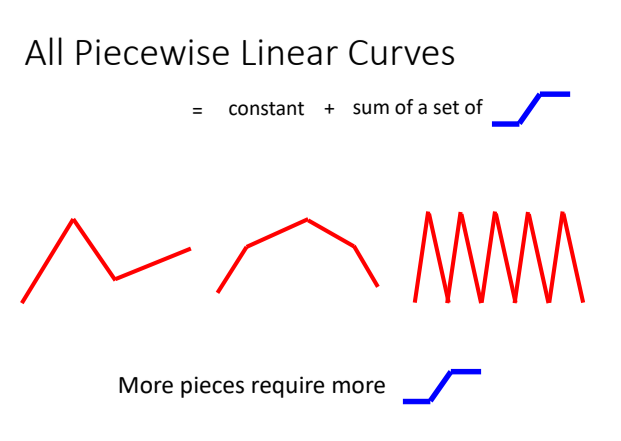
定义：由多段锯齿状的线段所组成的线

⇒可以看作是一个常数,再加上一堆蓝色的 Function（Hard Sigmoid)

用一条曲线来近似描述这条蓝色的曲线:Sigmoid函数（S型的function）

事实上，sigmoid的个数就是神经网络中的一层的neuron节点数(使用几个sigmoid是超参数）

结论：

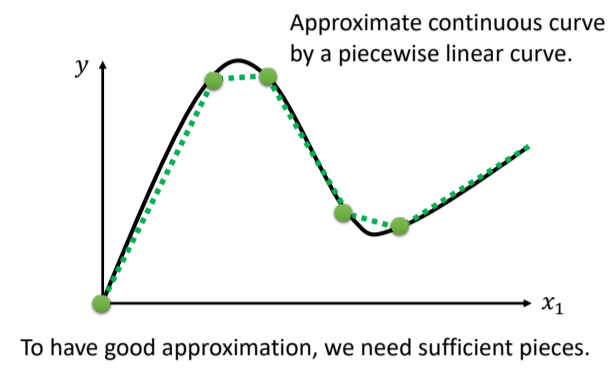
1. 可以用 Piecewise Linear 的 Curves,去逼近任何的连续的曲线
2. 每一个 Piecewise Linear 的 Curves,都可以用一大堆蓝色的 Function加上一个常量组合起来得到
3. 只要有足够的蓝色 Function 把它加起来,就可以变成任何连续的曲线

下面我们来详细介绍：

1.Hard sigmoid 函数

Beyond Piecewise Linear?

2.Sigmoid函数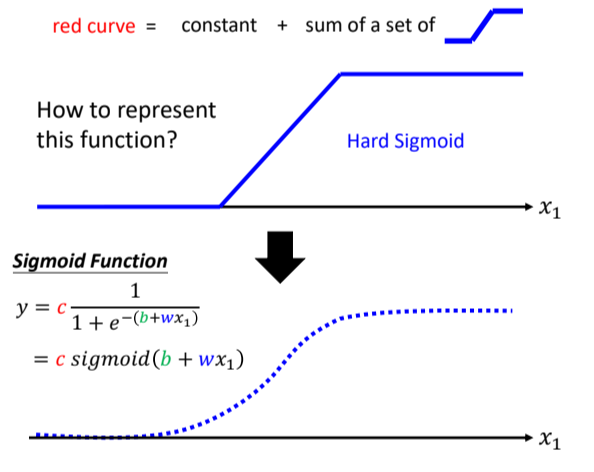

• 的值,趋近於正无穷大的⇒收敛在高度是 的地方
• 负的非常大的,分母的地方就会非常大⇒ 的值趋近于 0

调整 ，可以得到各种不同的sigmiod来逼近”蓝色function“，通过求和，最终近似各种不同的 Continuous 的 Function

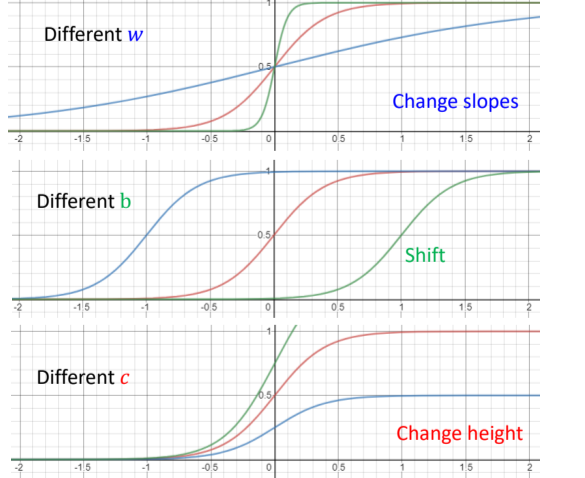
• 如果你今天改 你就会改变斜率你就会改变斜坡的坡度
• 如果你动了 你就可以把这一个 Sigmoid Function 左右移动
• 如果你改 你就可以改变它的高度

总结：利用若干个具有不同 w,b,c的Sigmoid函数与一个常数参数的组合，可以模拟任何一个连续的曲线（非线性函数）

接下来我们考虑扩展到多个特征：

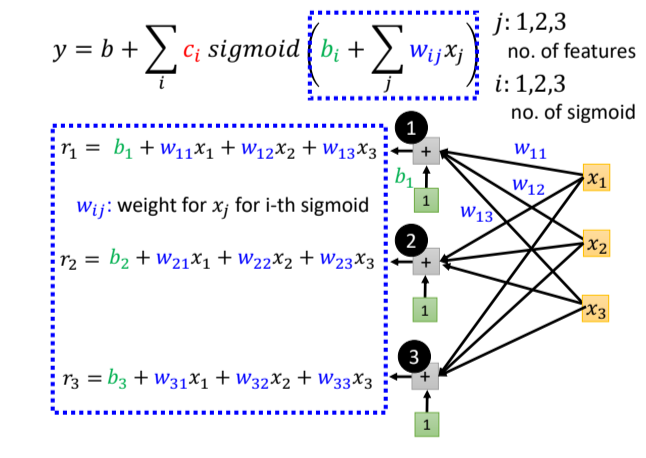
• j 等于 ,输入中 代表前一天的观看人数, 两天前观看人数, 三天前的观看人数
• 每一个 i 就代表了一个蓝色的 Function,现在每一个蓝色的 Function,都用一个 Sigmoid Function 来近似它
• 第个sigmoid给第个特征的权重

转化为矩阵计算+激活函数形式：

总之：

一般地，将所有的参数统称为.（包含 )

4.2. 写出loss函数

因为所有的参数统称为 ，所以Loss表示为

设定的方式没有不同。

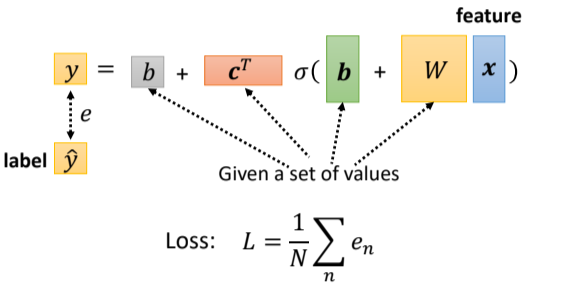
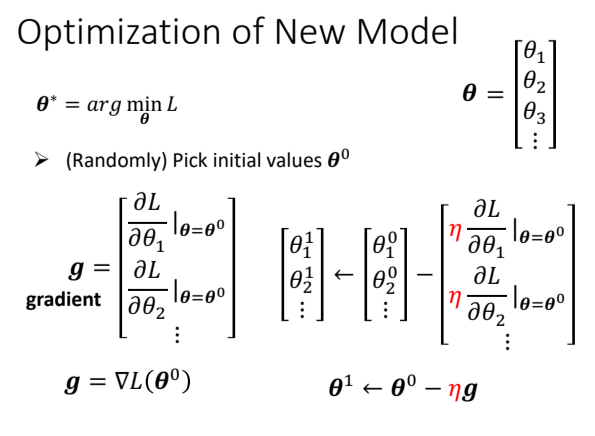
4.3.优化过程

仍然是梯度下降。

（1） 选定初始参数值（向量）

（2）对每个参数求偏导/微分（即，求梯度向量）

（3）更新参数，直至设定的次数

批训练Batch training

每次更新参数时，只使用1个batch里的数据计算Loss，求取梯度，更新参数

batch大小也是超参数

Update：每次更新一次参数叫做一次 Update,

Epoch：把所有的 Batch 都看过一遍,叫做一个 Epoch

❗为什么要分batch?(之后会说，待填坑…)

4.4模型变型⇒ReLU（Rectified Linear Unit，线性整流单元）

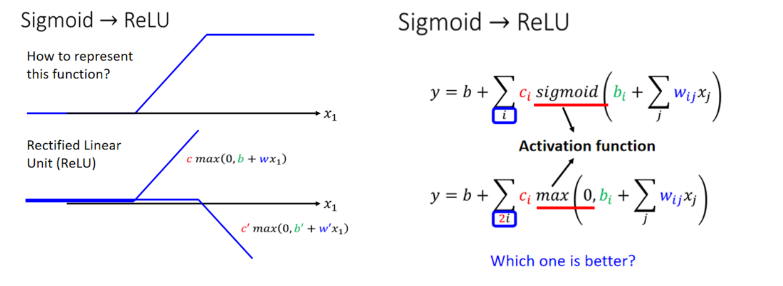
激活函数（Activation Function）

4.5模型变型⇒多加几层

做几次⇒模型的层数⇒超参数

5.正式引入：DeepLearning

有一个很有意思的问题：为什么神经网络要”深”而不要”胖”？

第二个有意思的问题：那既然要”深”，为什么不能无限”深”？——Overfitting(后面会讲，待填坑…)

Overfitting(过拟合)：在训练资料上有变好,但是在没看过的资料上没有变好