【从零开始的机器学习之旅】03-Regression Case

从零开始的机器学习之旅

-Regression Case

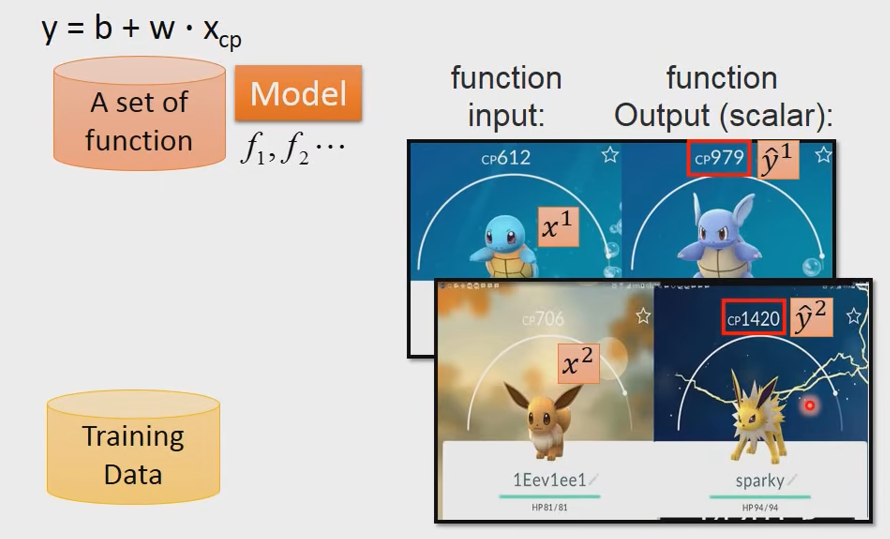
Example Application

• Estimating the Combat Power（CP） of a pokemon after evolution

我们知道MachineLearning 有三个步骤:

• Step1:function with unknown
• Step2:define loss from training data
• Step3:optimization

Step1:Model

Step2:Goodness of Function

Loss function L：

我们把L(w,b)画出来，红色代表值越大，越不好；蓝色代表值越小，越好。

Step3:Best Function

最暴力的方法，我们穷举所有的和，看那一组会使得最小，我们把使得最小的那一组定义为和

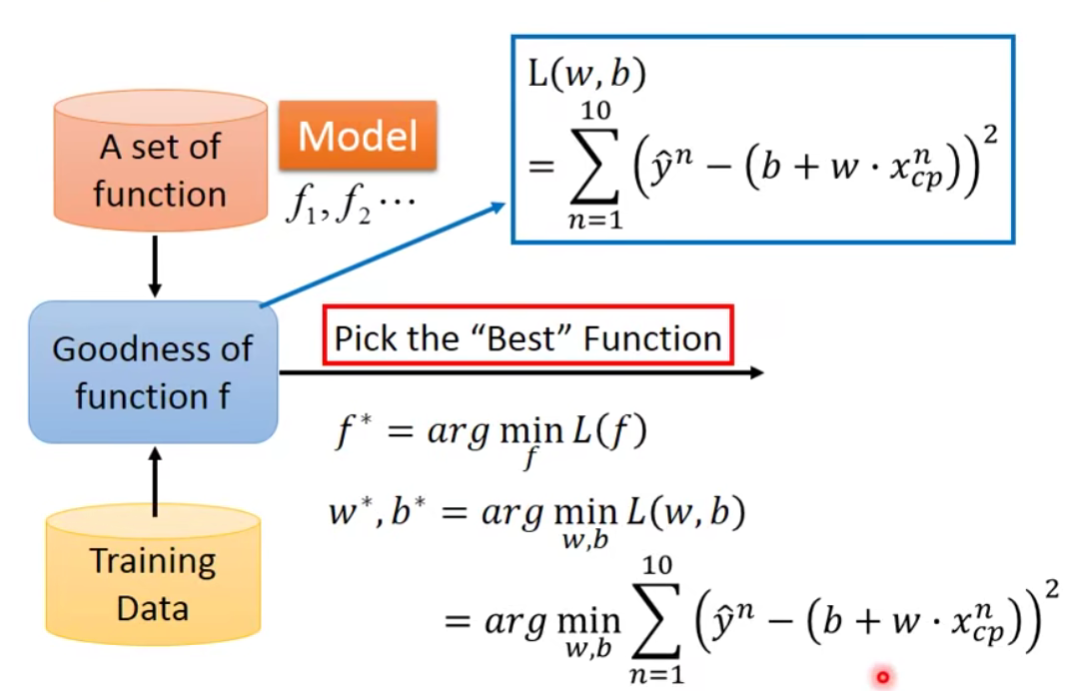
当然我们有更好的方法使得最小，那就是Gradient Descent

Gradient Descent

1. 先考虑一个毕竟简单的情况：

• Consider loss function L(w) with one parameter w：

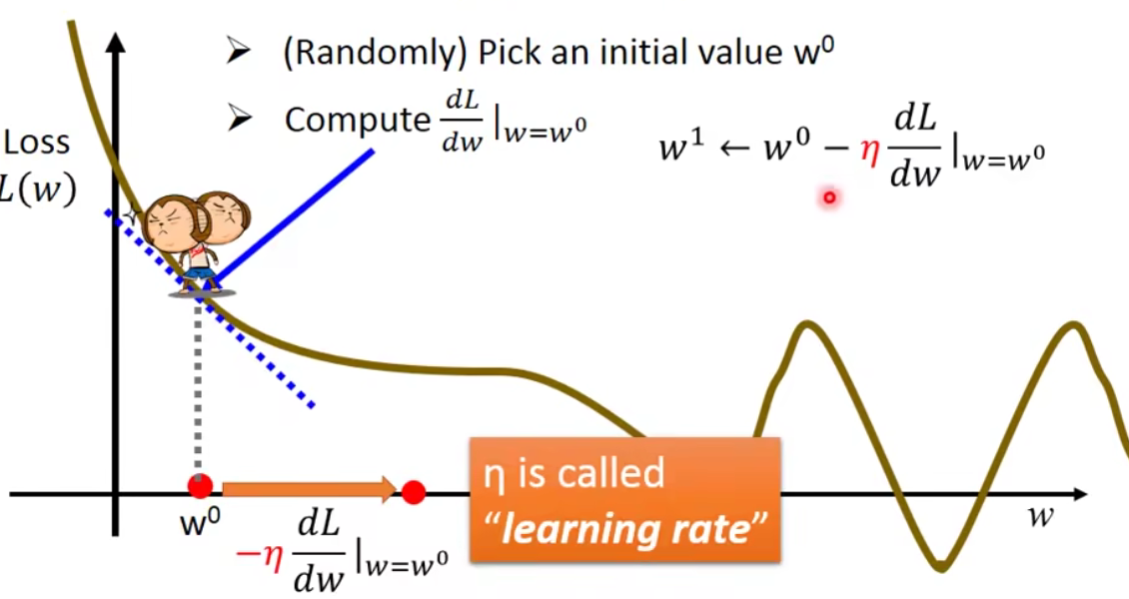
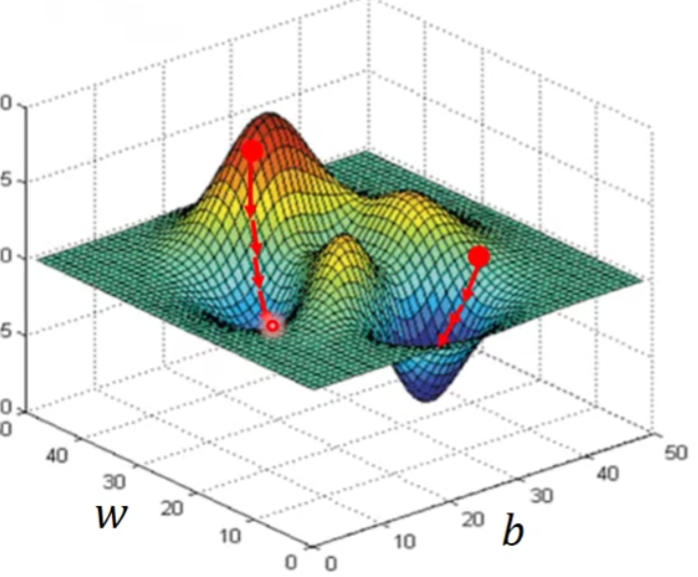
经过很多次如下操作只能呢，我们可能会遇到Local minima的问题

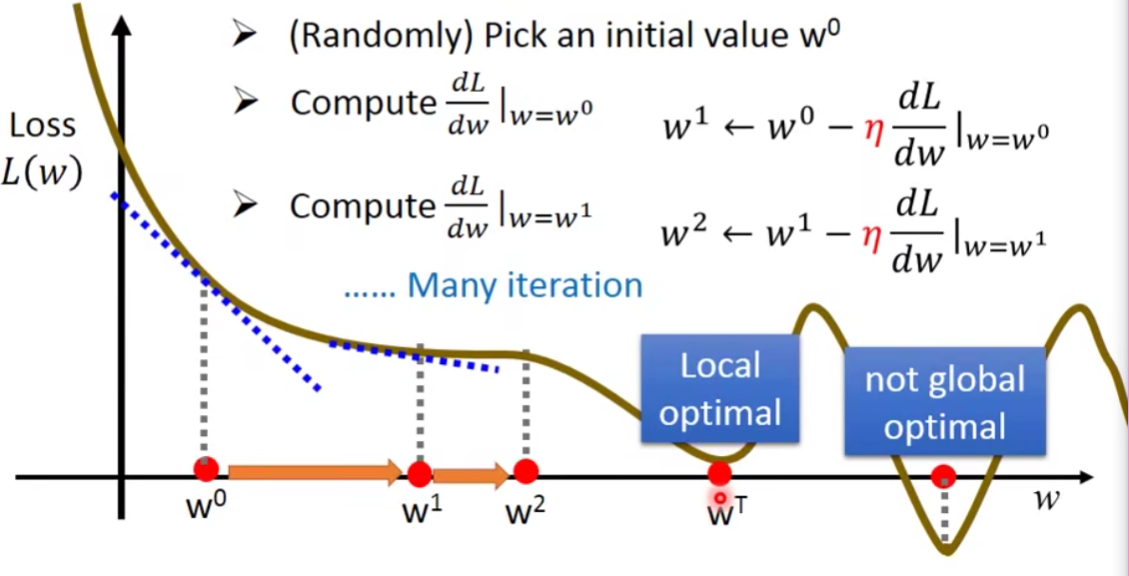
很幸运的是，在Linear regression的问题上面呢，是没有Local minia的问题啦。

2.考虑更多的参数的情况

• How about two parameters?

gradient：

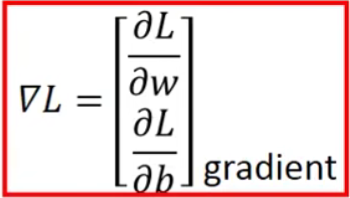
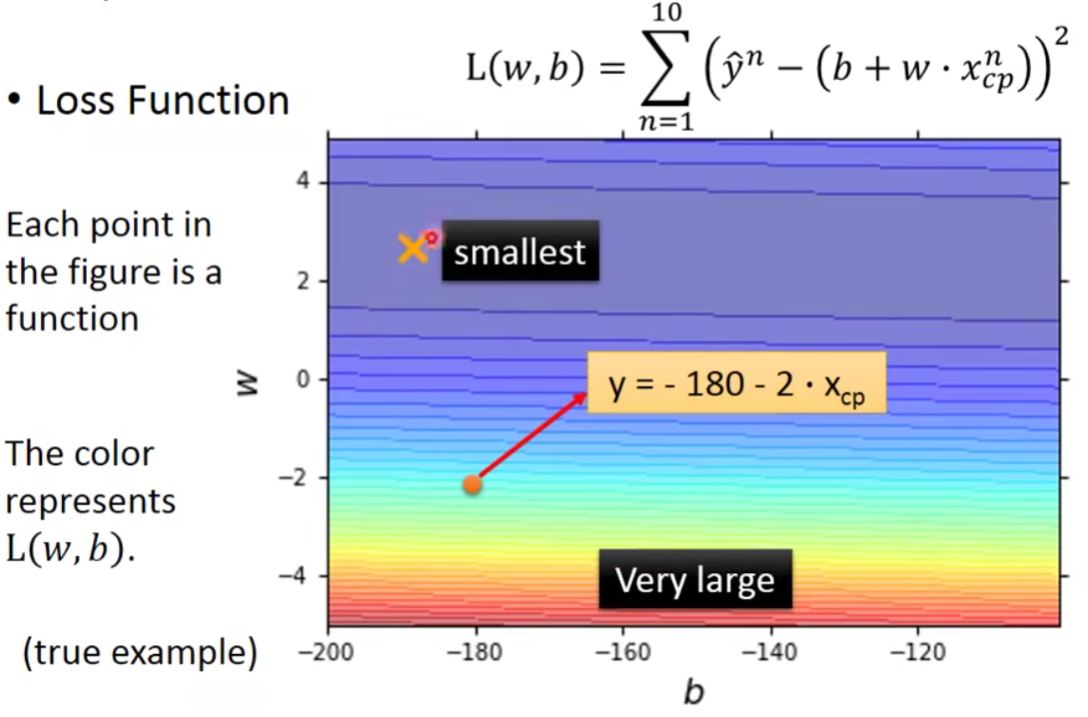
现在让我们来visualize一下刚刚做的事情：

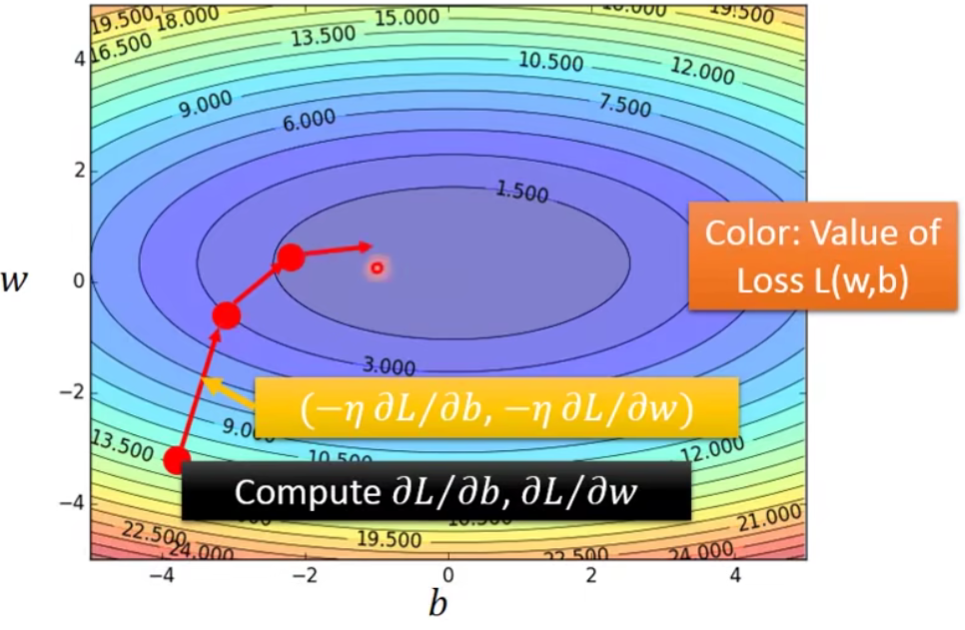
• Worry?

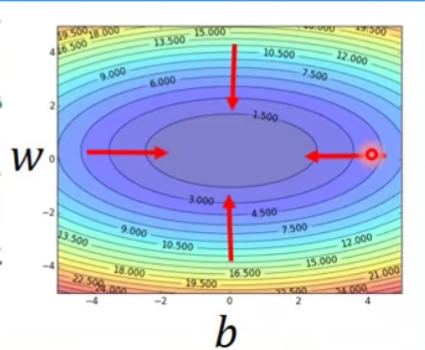
Don’t worry.In linear regression the loss function L is convex(凸).——No local optimal.

它的等高线呢，都是会长成下面这个样子，无论怎么随机选取初始值，最后都会找到同一组最优解的参数。

• Formulation of and

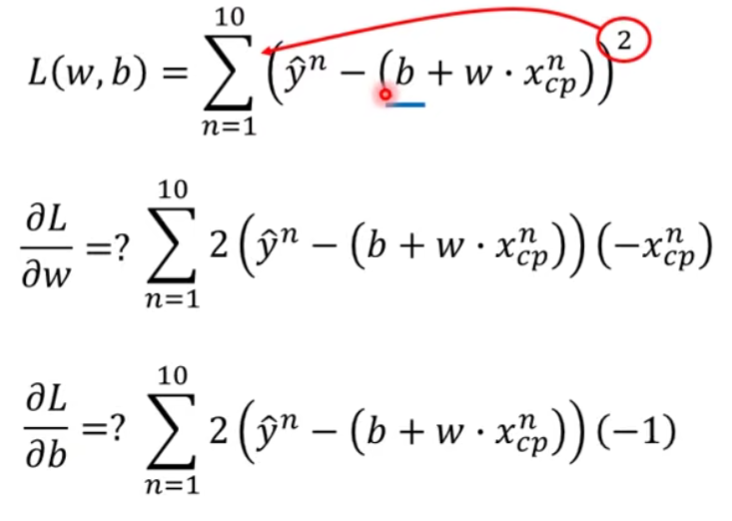
How’s the results?

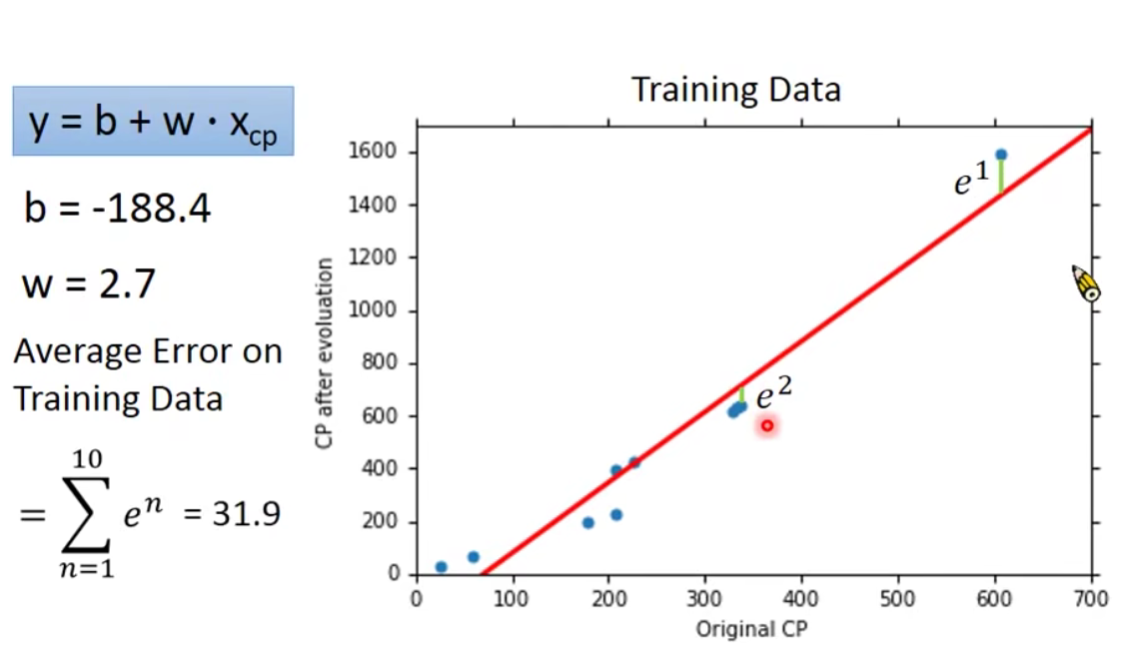
但是以上结果并不是我们真正关心的。

What we really care about is the error on new data(testing data)

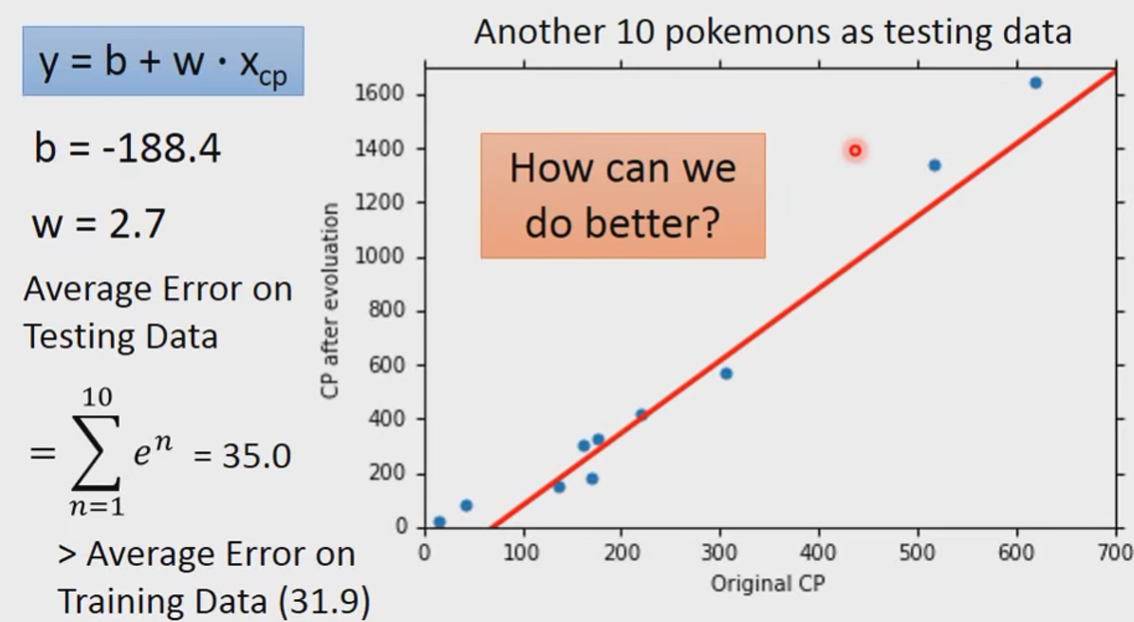
我们发现初始cp值比较小或者比较大的时候预测是比较不准确的。

我们可以猜测，或许真正好的Model不应该是一条直线，而应该是别的。

引入一个二次项：

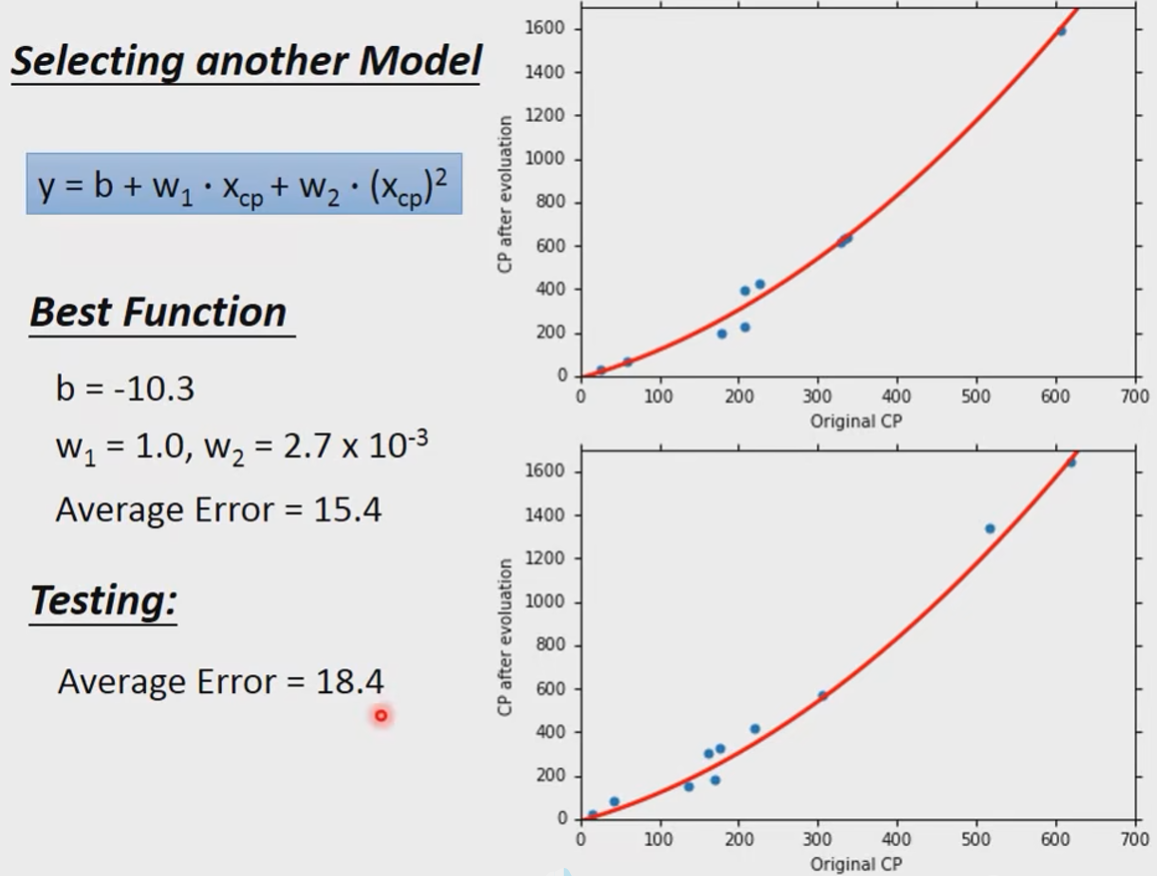
继续尝试，引入三次项：

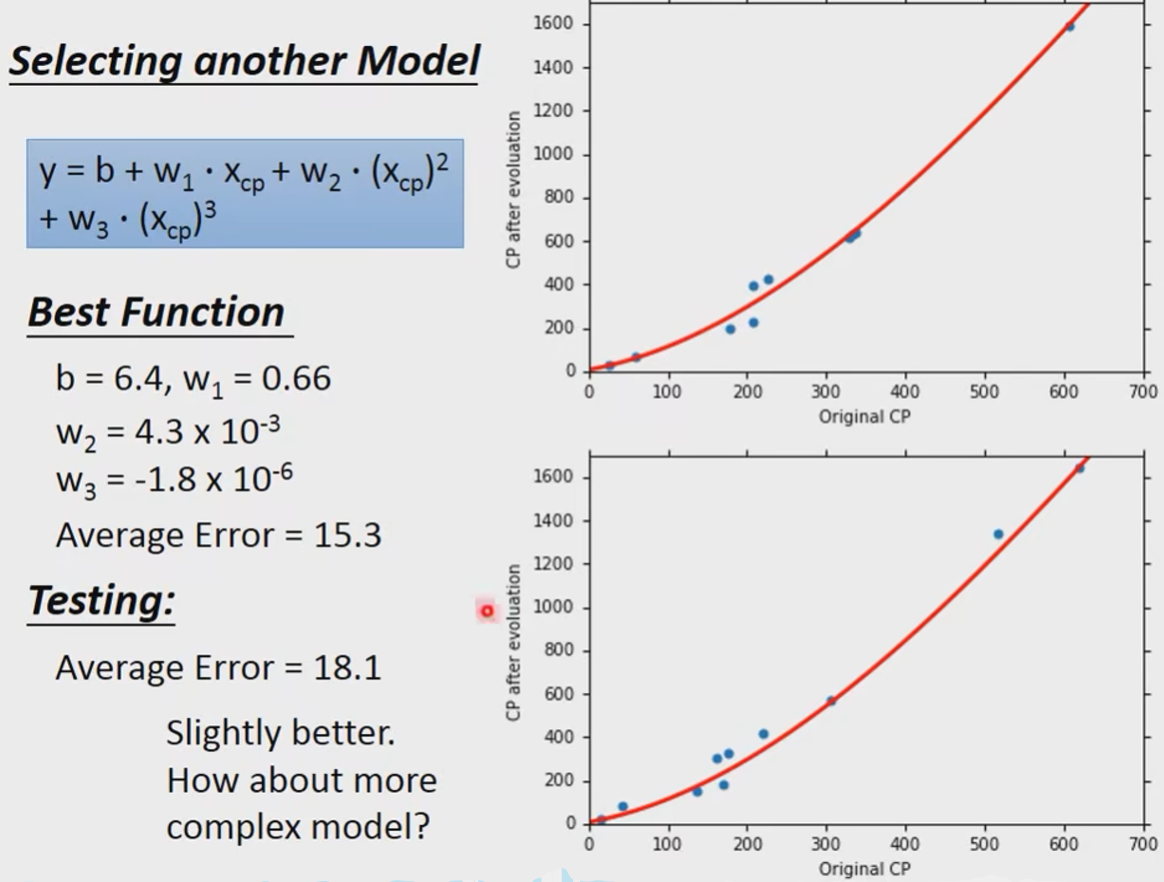
我们发现结果比之前好了，我们继续尝试更复杂的，引入四次项：

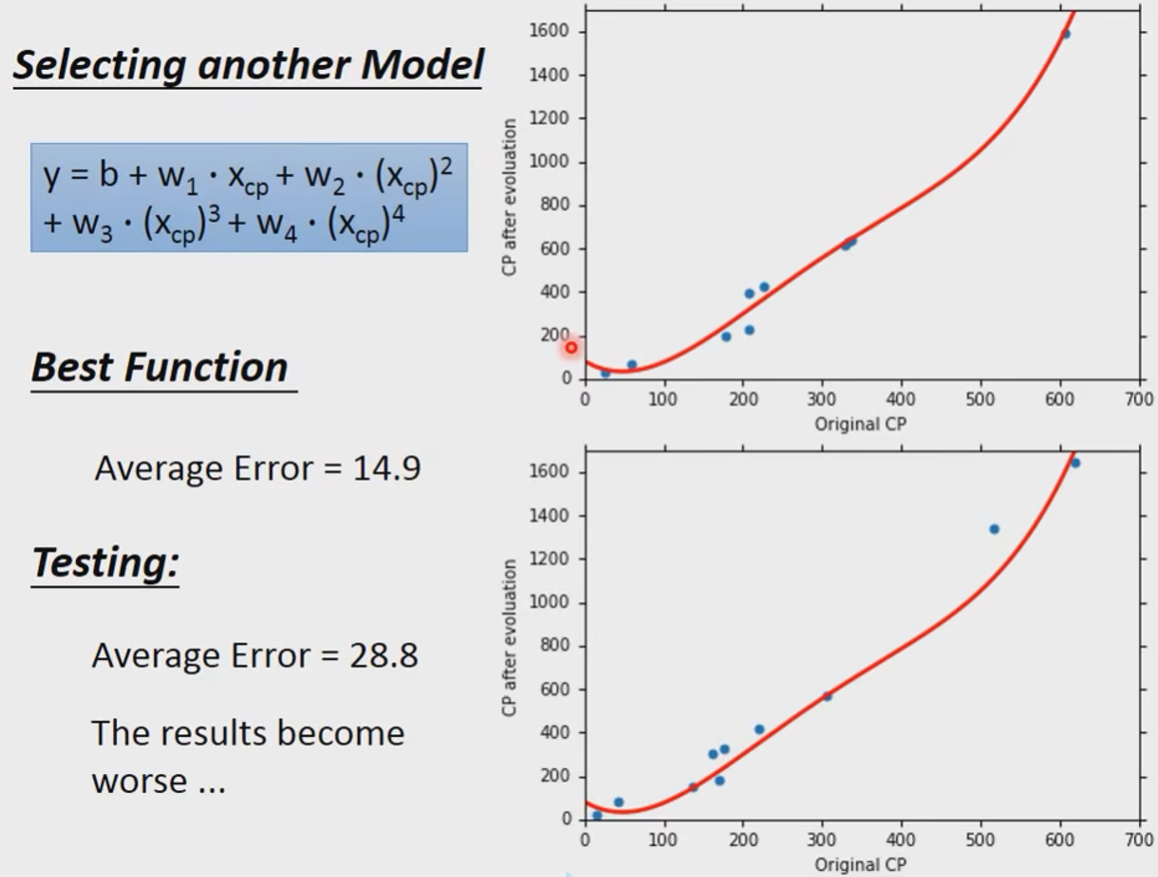
奇怪的是在training data上确实更好了，但是在testing data上却更糟糕了，这啥怎么回事呢？

我们再尝试一下更复杂的试试。

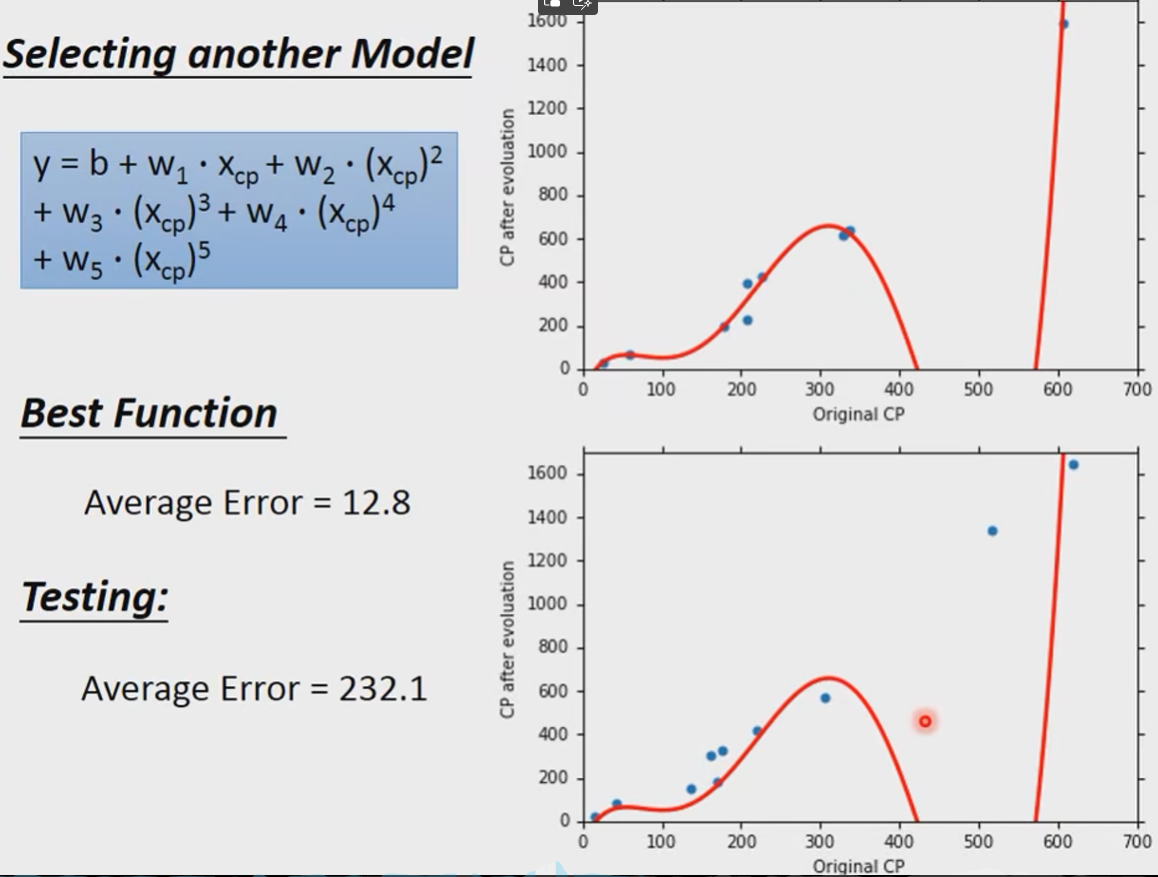
我们发现结果更加糟糕了。

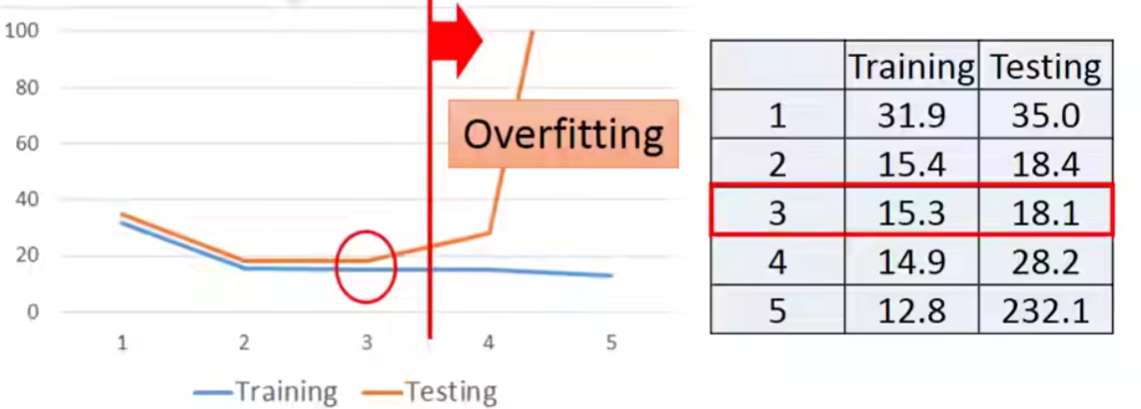
到目前为止，我们一共尝试了5个不同的model:

在training data上面呢，越复杂的model最后结果越好。

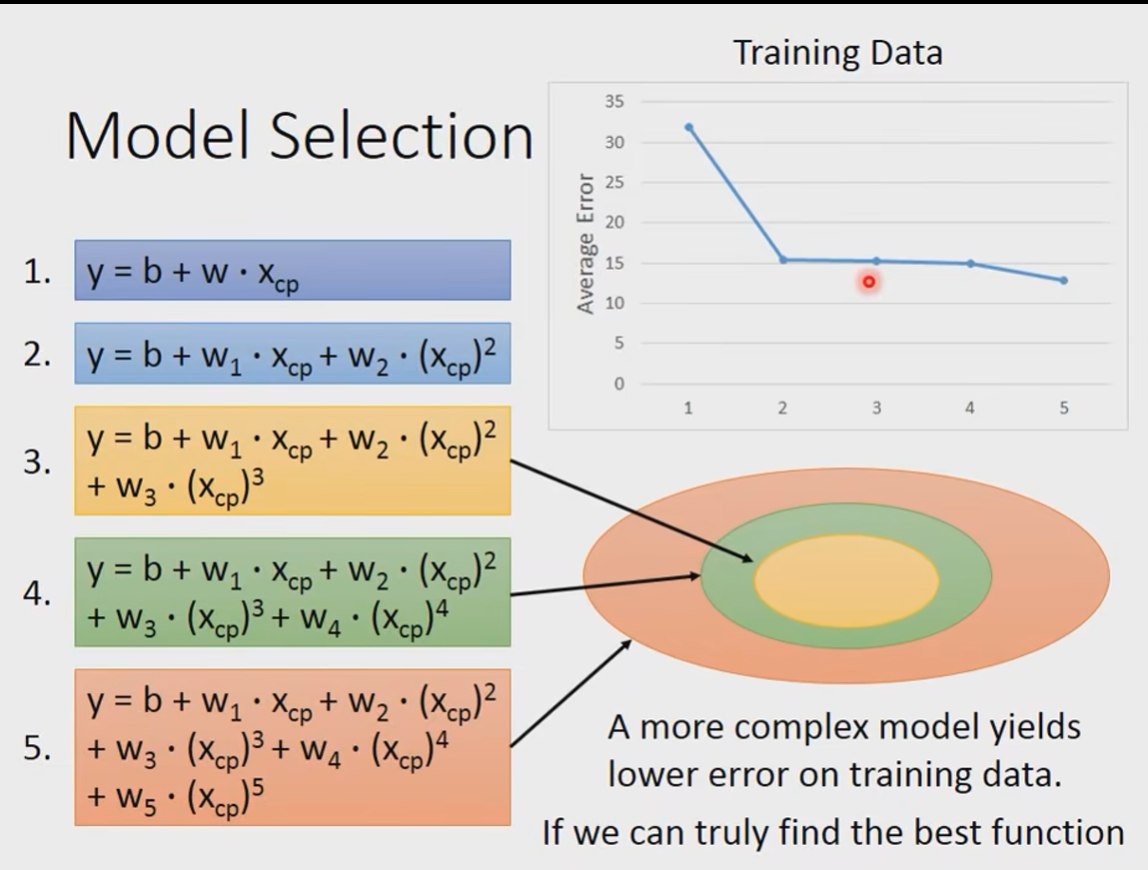
但是在testing data上面呢？

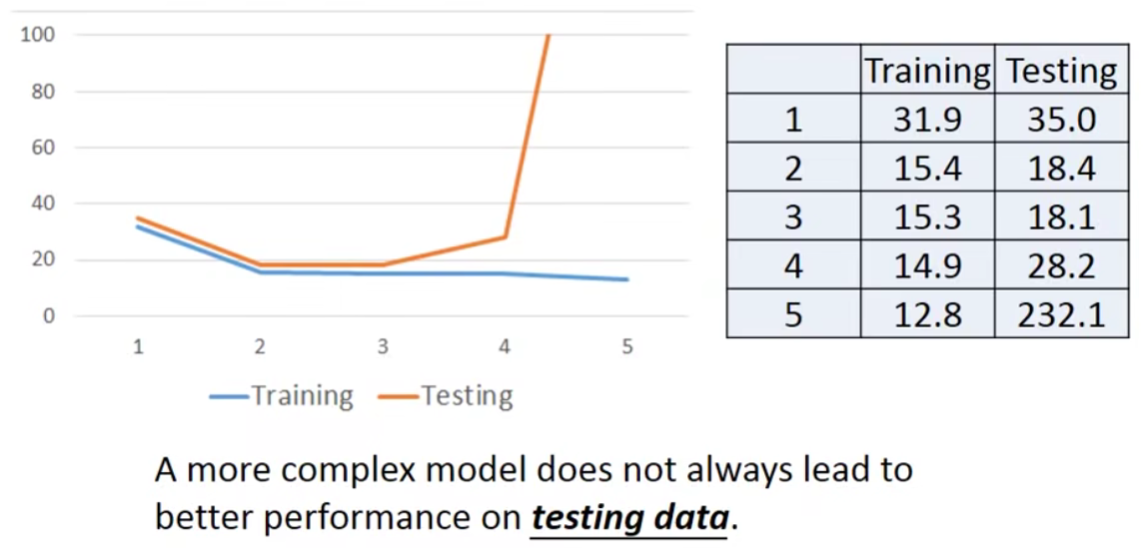
Overfitting

This is Overfitting——>Select suitalbe model.

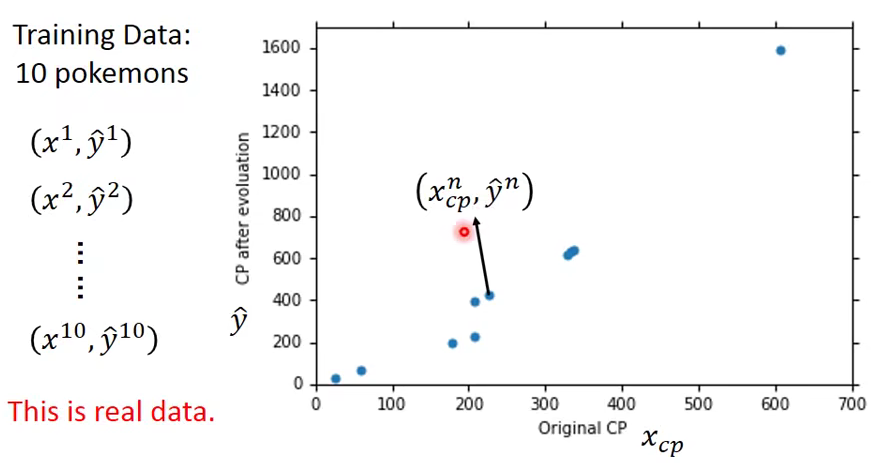
刚刚我们只收集了10只宝可梦是数据，其实太少了。

Let’s collect more data…

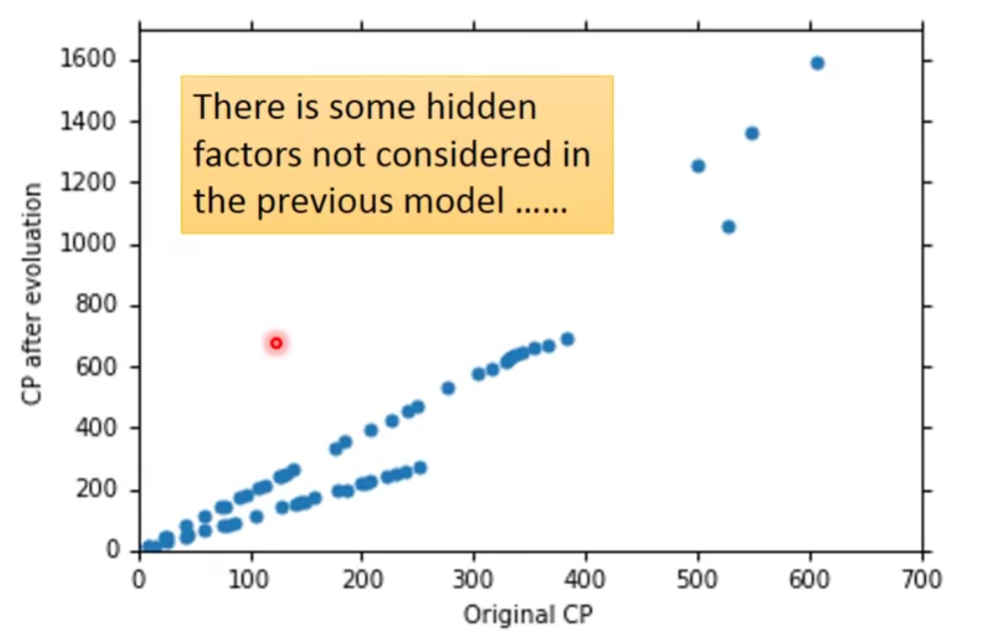
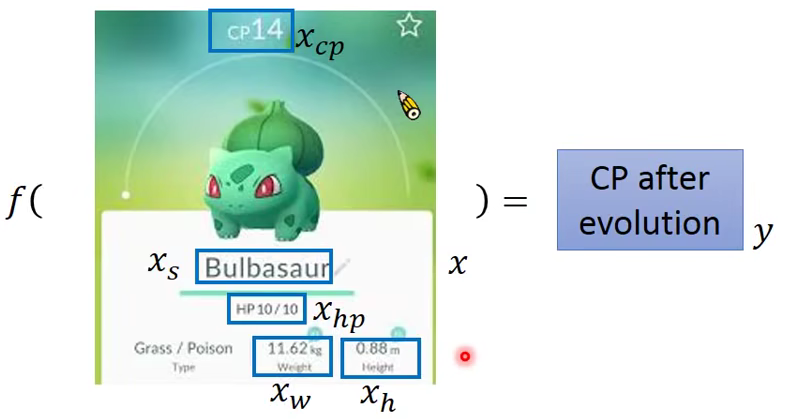
What are the hidden factors?——宝可梦的物种

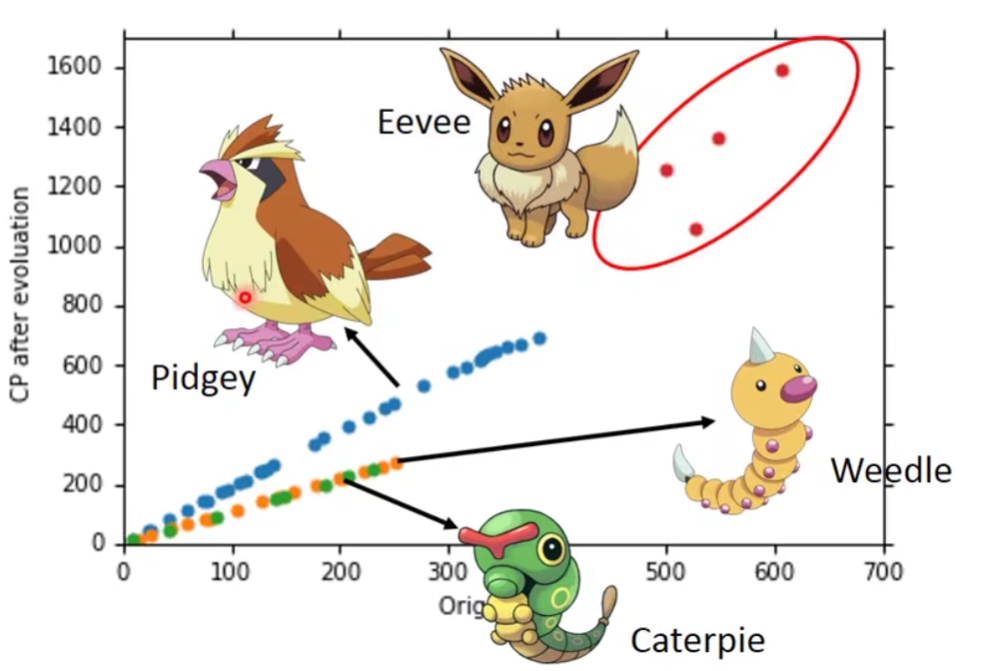
我们意识到这个问题，那么说明我们一开始设计的model是不好的。

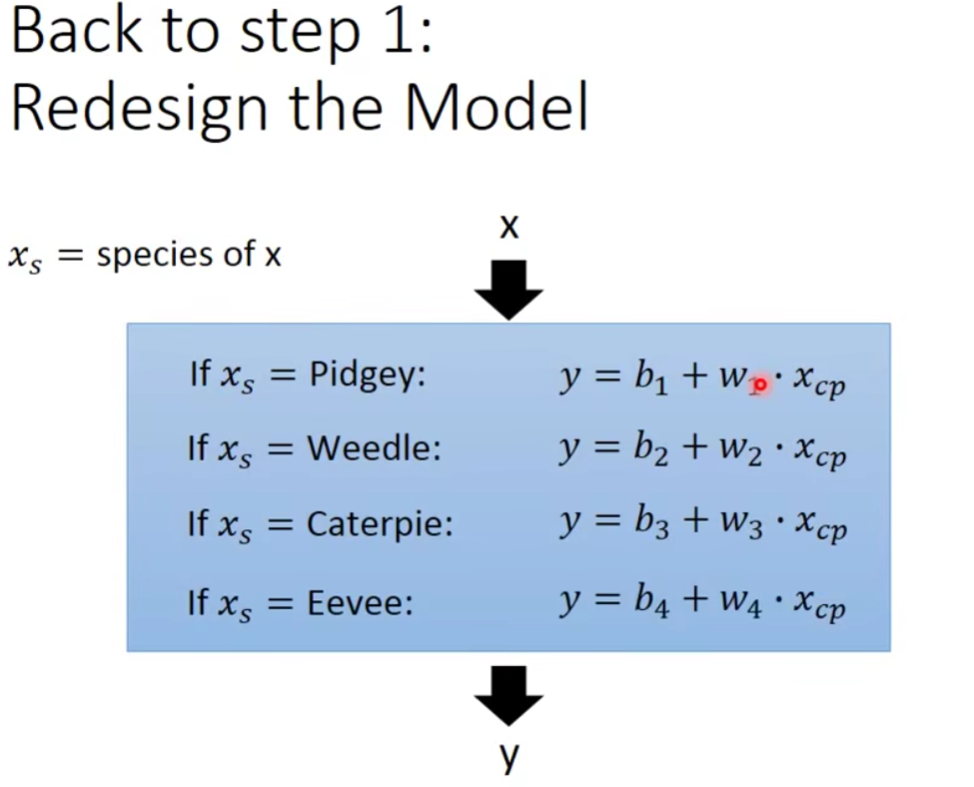
既然我们用if来写，那么我们是linear model吗？

其实是可以的，我们写成下面这种形式：

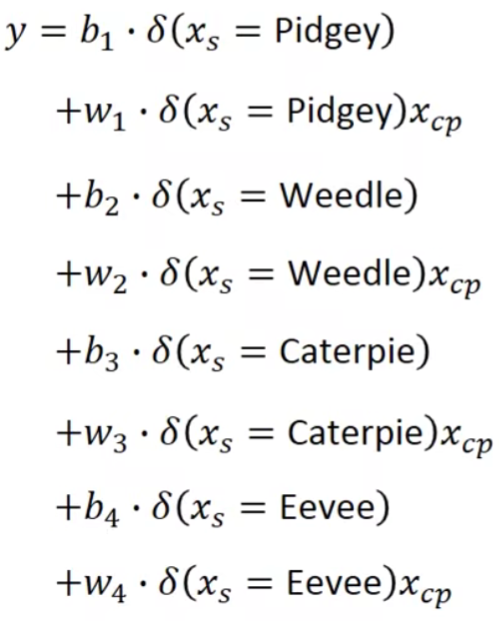
这是什么意思呢？

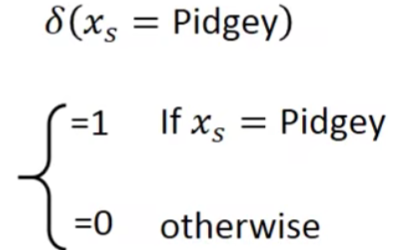
这样我们就可以把上面的if的形式写成linear function的形式啦。

按照上面只有做结果怎么样呢？

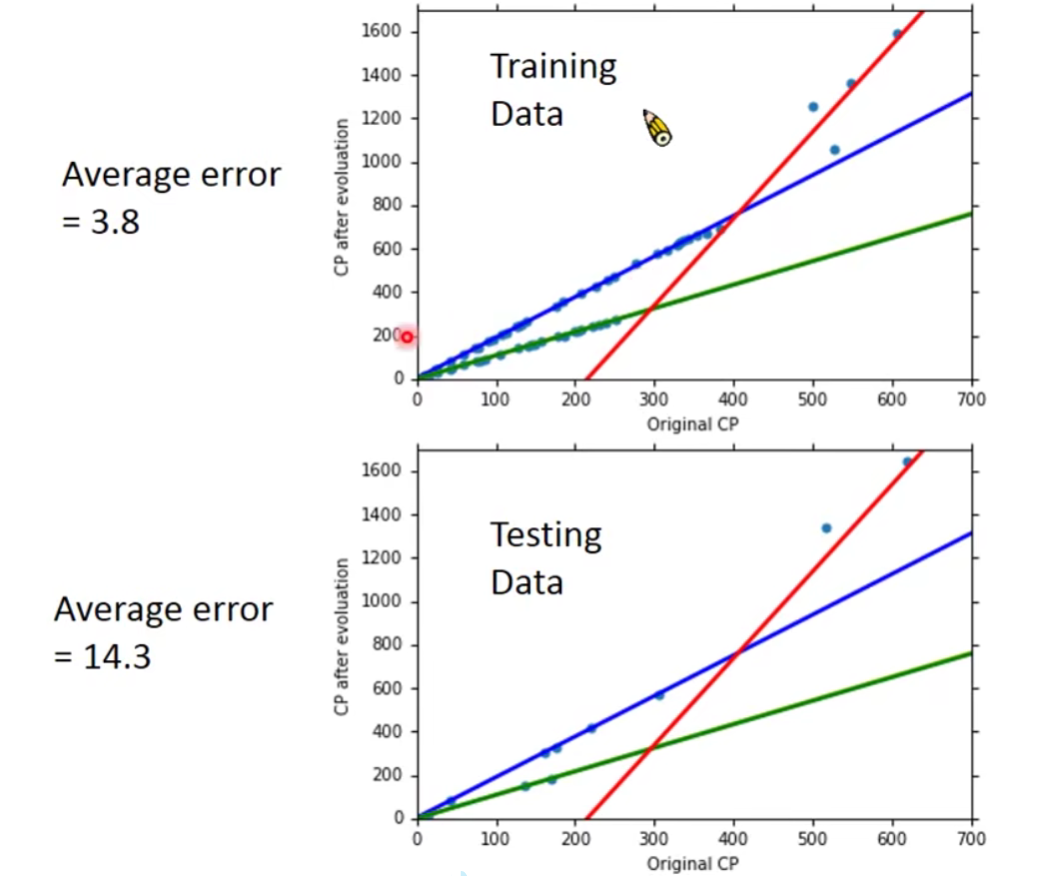
我们发现还是有一点偏差。

Are there any other hidden factors?

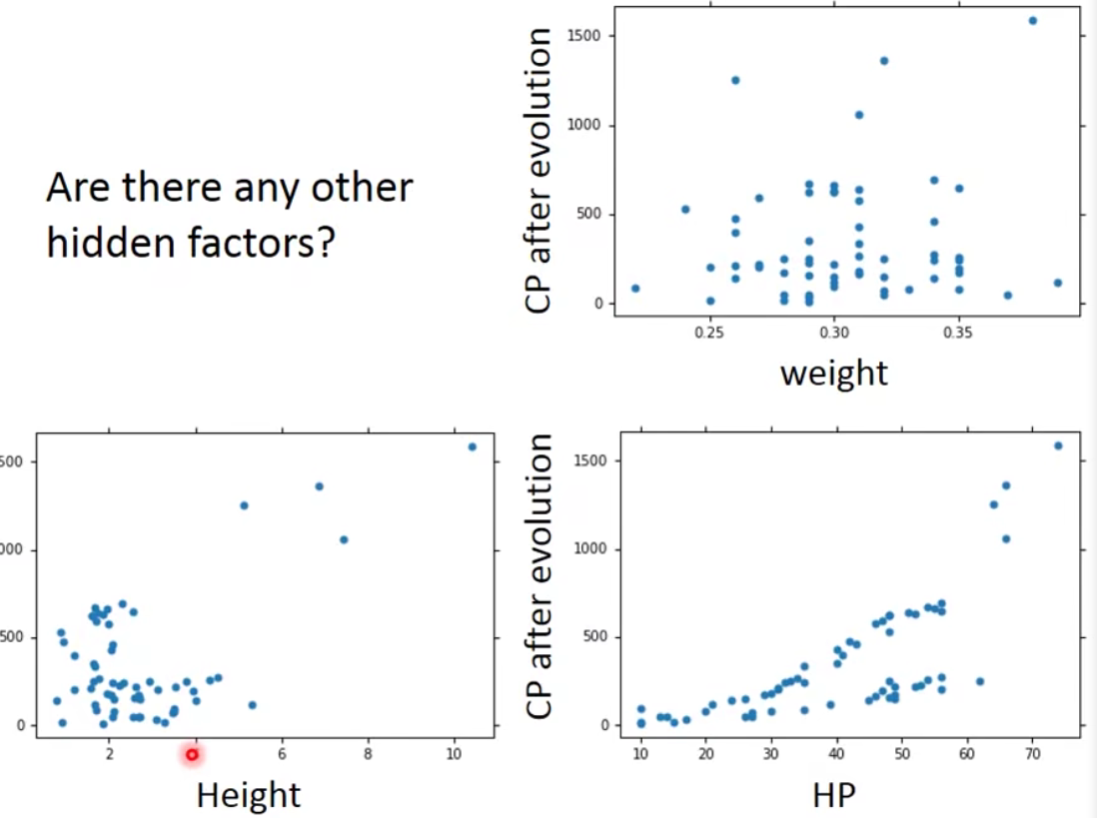
我们把这些也考虑进去：

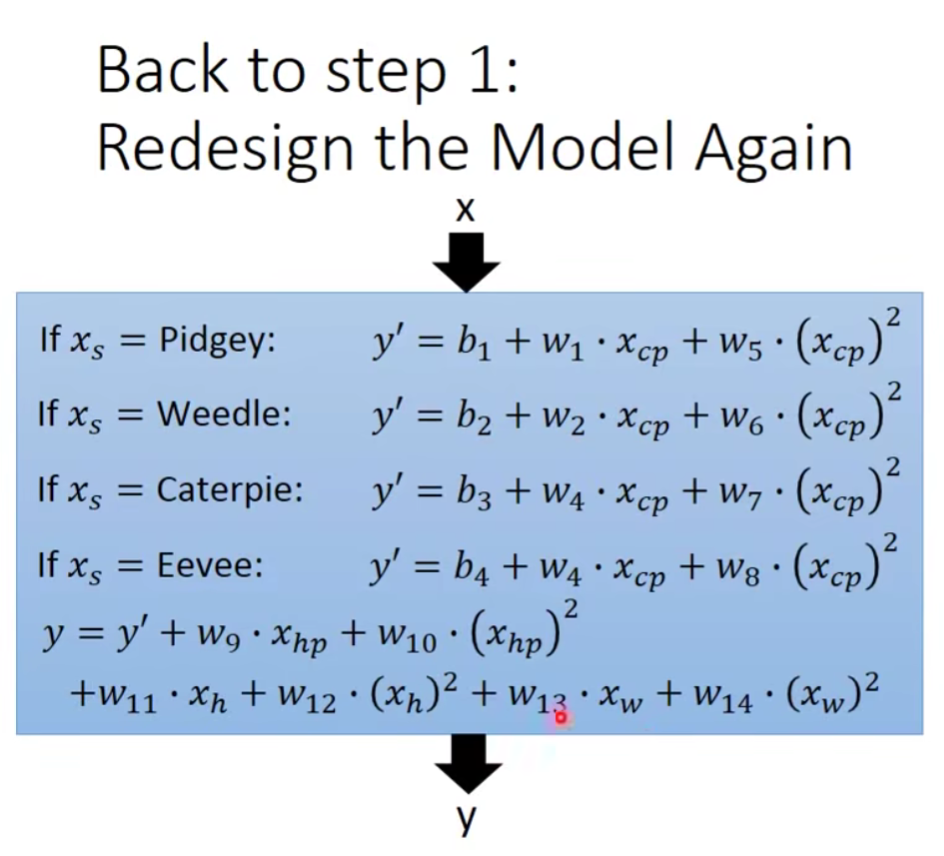
结果是：

我们考虑去重新定义我们的损失函数，想要找到更好的一组参数:

Regularization

Regularization，中文翻译过来可以称为正则化，或者是规范化。什么是规则？闭卷考试中不能查书，这就是规则，一个限制。同理，在这里，规则化就是说给损失函数 加上一些限制，通过这种规则去规范他们再接下来的循环迭代中，不要自我膨胀。

通过分析，我们可以看出，。我们对代价函数增加一个限制条件，限制其较高次的参数大小不能过大。

当越接近0的时候呢，我们的曲线越平滑。

那么为什么更喜欢平滑的曲线呢？

• If some noises corrupt input when testing —— A smoother function has less influence.

但是也不能太平滑喔：

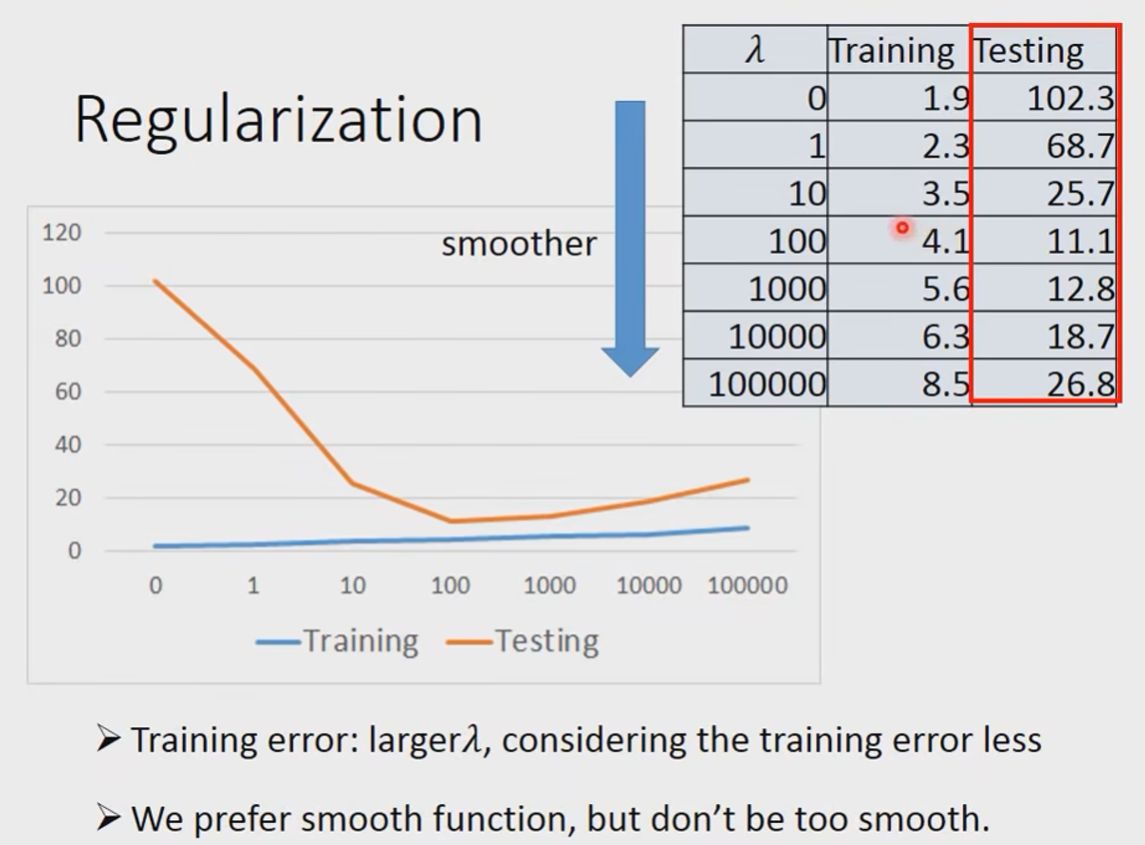
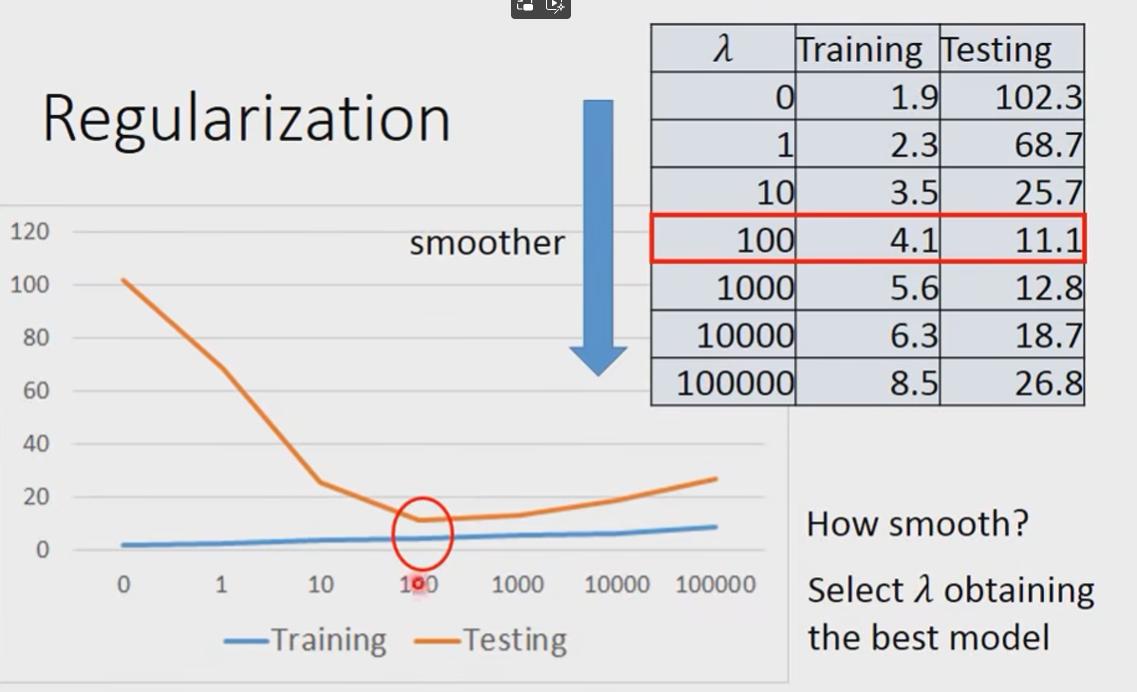
现在的问题又来到了：How smooth？

• Select obtatining the best model

Conclusion & Following Lectures

• Pokemon：Original CP and species almost decide the CP after evolution(there are probably other hidden factors)
• Gradient descent
  • Following lectures：theory and tips
• Overfitting and Regularization
  • Following lectures：more theory behine these
• We finally get average error = 11.1 on the testing data
  • How about another set of new data?Underestumate?Overestimate?
  • Fellowing lectures: validation