【从零开始的机器学习之旅】04-Classification:Probabilistic Generative Model(概率生成模型)

从零开始的机器学习之旅

---

-Classification: Probabilistic Generative Model(概率生成模型)

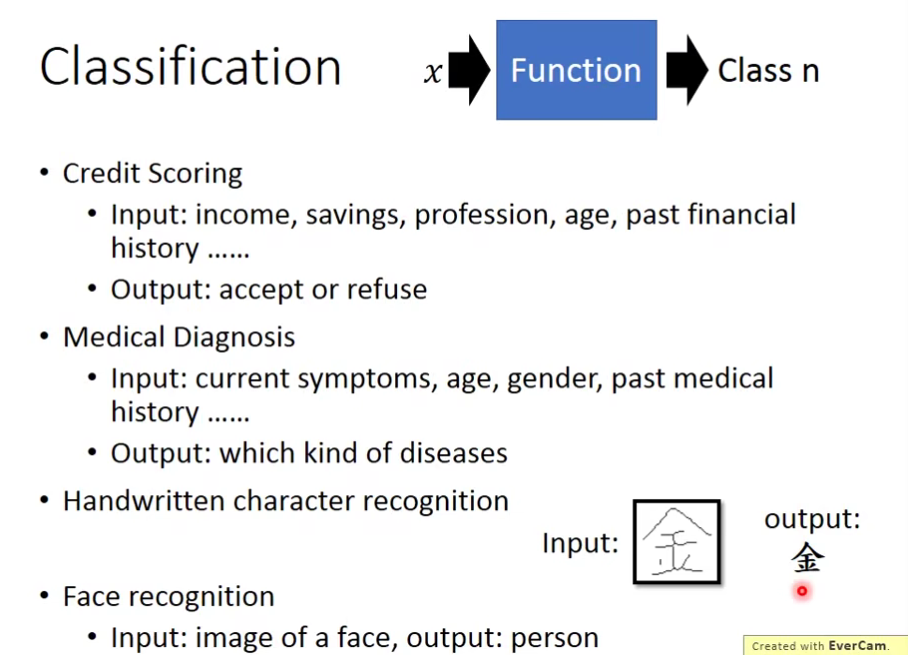
Example Application

我们来讲一个有趣的案例：宝可梦分类

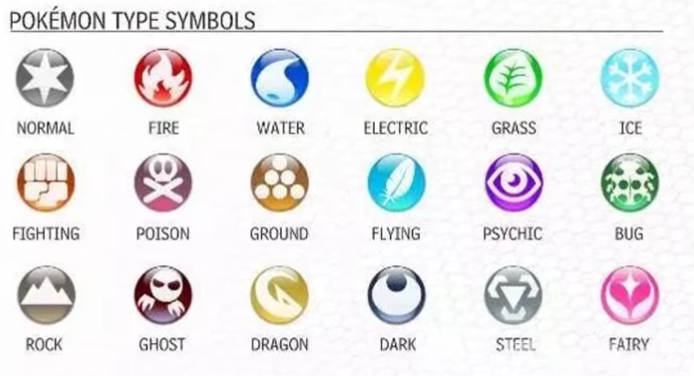
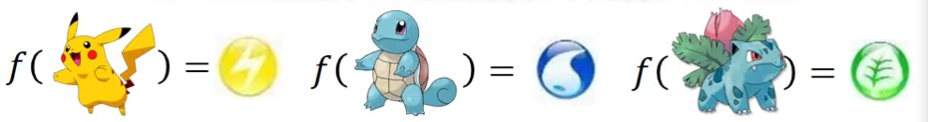
那么现在我们遇到第一个问题，如何把一个宝可梦输入进去呢？我们知道要输入进去我们得是数值呀。

那么我们要怎么把一个宝可梦用数字来表示呢？

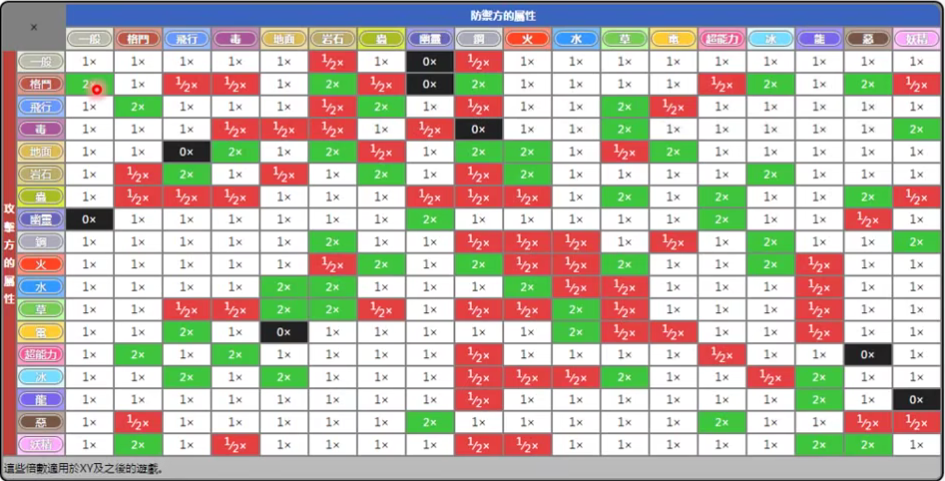
1.How to do Classification

• Training data for Classification

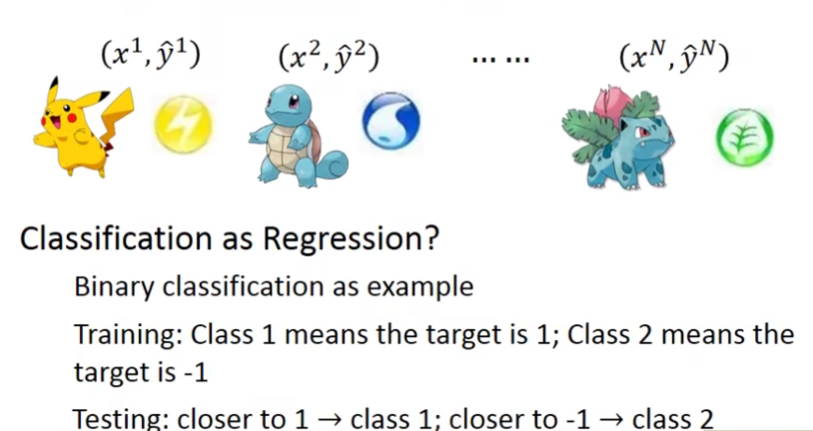
2.Classification as Regression?

那么如果把classification的问题当作regression的问题来硬解会遇到什么问题呢？

先来看第一种情况：

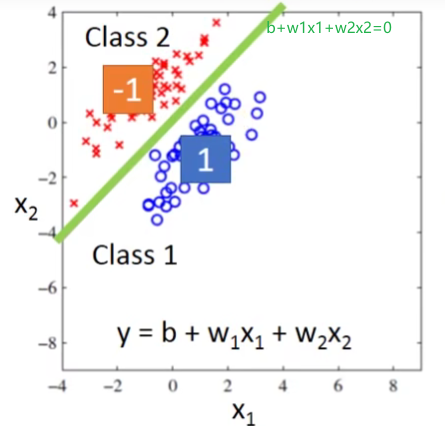
这样子看上去分的还不错，但是如果我们遇到的是下面这种情况呢？

我们如果用regression来做我们得到的不会是绿色那一条线，而会是紫色的那条。

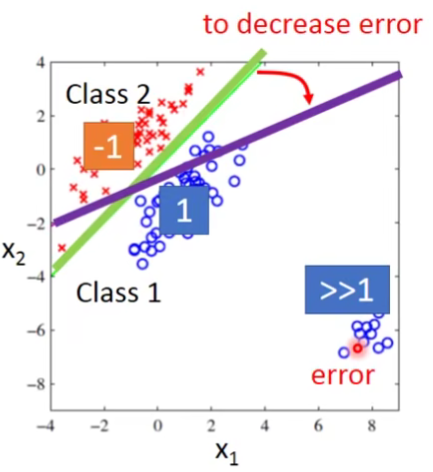
其实除了上述说的二分类问题的第二种情况会遇到问题，我们的多分类问题也无法处理。

• Multiple class:Class1 means the target is 1;Class2 means the target is 2;Class3 means the target is 3… … problematic

3.Ideal Alternatives

但是这个loss function没有办法微分，是无法用gradient descent的方法去解的，当然有Perceptron、SVM这些方法可以用，但这里先用另外一个solution来解决这个问题

4.Solution：Generative model

我们先来看一个简单的问题：

假设我们考虑一个二元分类的问题，我们拿到一个input x，想要知道这个x属于class 1或class 2的概率

实际上就是一个贝叶斯公式，x属于class 1的概率就等于class 1自身发生的概率乘上在class 1里取出x这种颜色的球的概率除以在class 1和 class 2里取出x这种颜色的球的概率(后者是全概率公式)

贝叶斯公式=单条路径概率/所有路径概率和

  graph LR;
      摸球-->从Box1里摸的概率;
      从Box1里摸的概率-->Box1;
      Box1-->在Box1里摸到x的概率;
      摸球-->从Box2里摸的概率;
      从Box2里摸的概率-->Box2;
      Box2-->在Box2里摸到x的概率;
      在Box1里摸到x的概率-->摸到x
      在Box2里摸到x的概率-->摸到x

我们把Boxes换成Classes:

我们想知道x属于class 1或是class 2的概率，只需要知道4个值：

流程图简化如下：

graph LR
begin-->A["P(C1)"]
begin-->B["P(C2)"]
A["P(C1)"]-->Class1
B["P(C2)"]-->Class2
Class1--> x
Class2--> x

于是我们得到：(分母为全概率公式)：

• x属于Class 1的概率为第一条路径除以两条路径和：
• x属于Class 2的概率为第二条路径除以两条路径和：

这一整套想法叫做Generative model(生成模型)，为什么叫它Generative model呢？因为有这个model的话，就可以拿它来generate生成x(如果你可以计算出每一个x出现的概率，就可以用这个distribution分布来生成x、sample x出来)

第一个问题：从某一个类中sample出一个宝可梦的概率是多少呢？

4.1 Prior(先验概率)

预先知道事件的发生概率,在这里是和

4.2 Probability from Class

如何求和呢？

第二个问题：给你一个宝可梦，问你这个宝可梦从某个Class中sample出来的概率。

假设我们的x是一只新来的海龟，它显然是水系的，但是在我们79只水系的宝可梦training data里面根本就没有海龟，所以挑一只海龟出来的可能性根本就是0啊！所以该怎么办呢？

• 我们用一个向量代表一个宝可梦的feature

假设海龟的vector是[103 45]，虽然这个点在已有的数据里并没有出现过，但是不可以认为它出现的概率为0，我们需要用已有的数据去估测海龟出现的可能性

Gaussian distribution(正态分布)

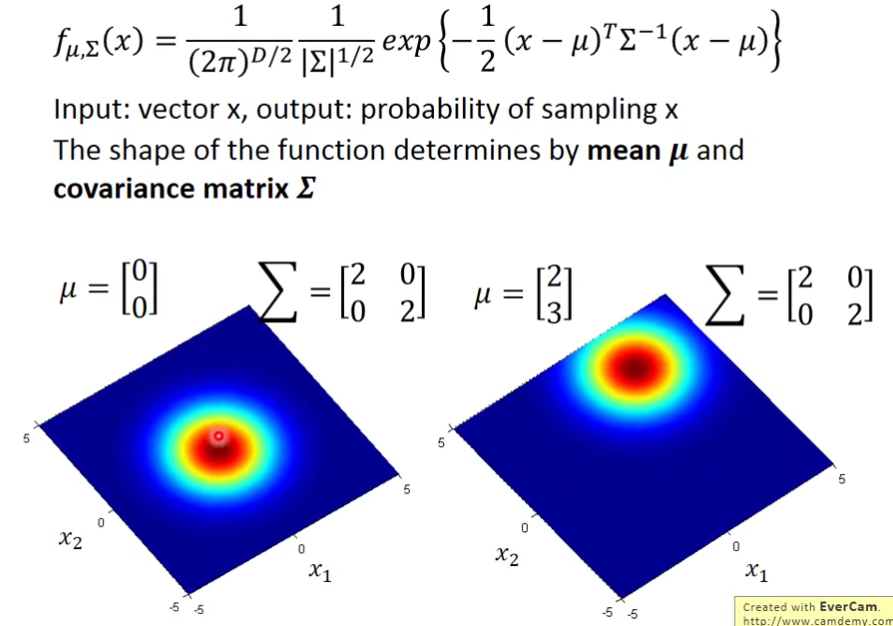
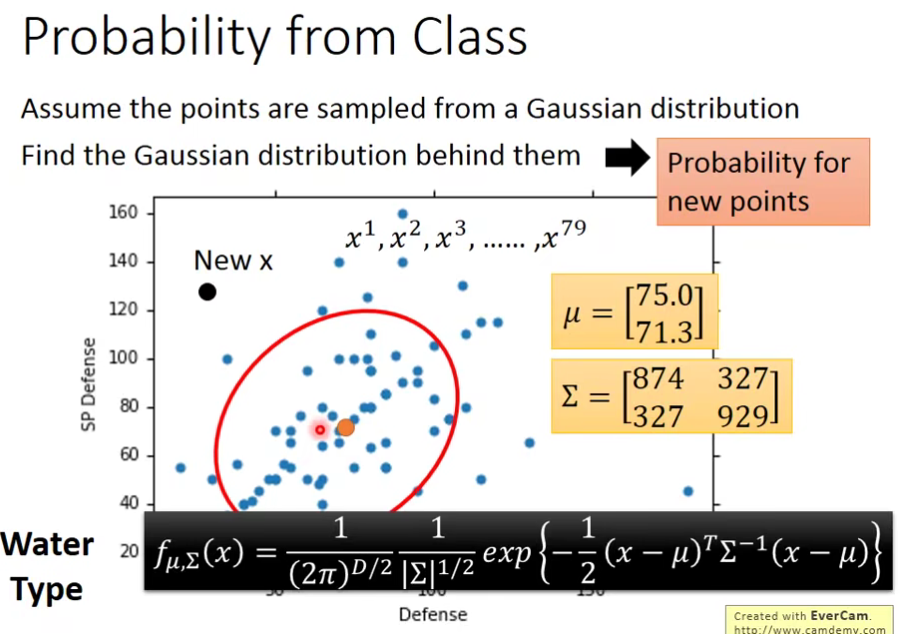
现在的问题是：怎么去找这个和

任何一个Gaussian都可以simple出这79个点，只不过说某些点几率高，某些点几率低。也就是说它们simple出每个点的可能性是不一样的。

• The Gaussian with any mean and convariance maxtrix(协方差矩阵) can generate these point. Different Likelihood
• Likelihood of a Gaussian with mean and covariance matrix = the probablity of the Gaussian samples

(每一个点都是独立产生的)

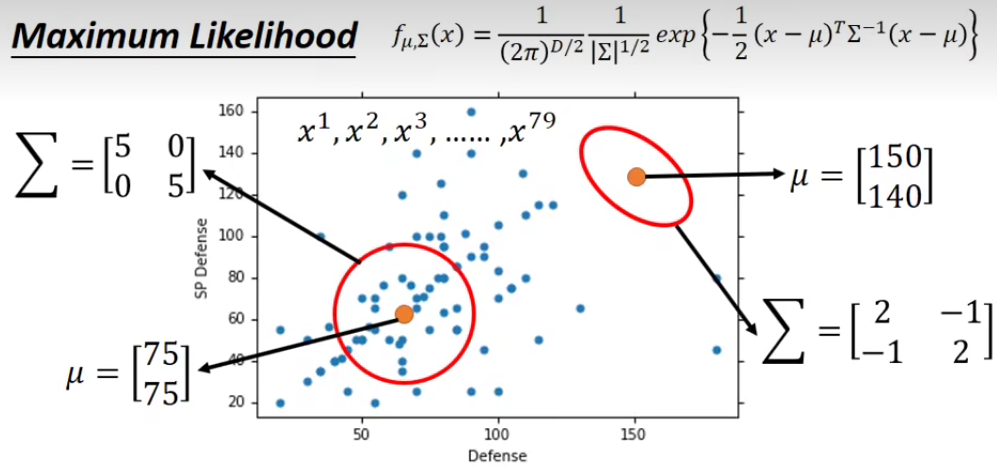
4.3 Maximum Likelihood(最大似然)

极大似然估计（Maximum likelihood estimation, 简称MLE）也称最大似然估计。是一种概率论在统计学的应用，它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次试验，观察其结果，利用结果推出参数的大概值。极大似然估计是建立在这样的思想上：已知某个参数能使这个样本出现的概率最大，我们当然不会再去选择其他小概率的样本，所以干脆就把这个参数作为估计的真实值。

在这个例子中就是要找出最特殊的那对和，从它们共同决定的高斯函数中再次采样出79个点，使得到的分布情况与当前已知79点的分布情况相同“这件事情发生的可能性最大。

那么我们现在就需要去找到一个使得产生这79点的概率是最大的。

按照上面的方法我们去算出最好的一组：

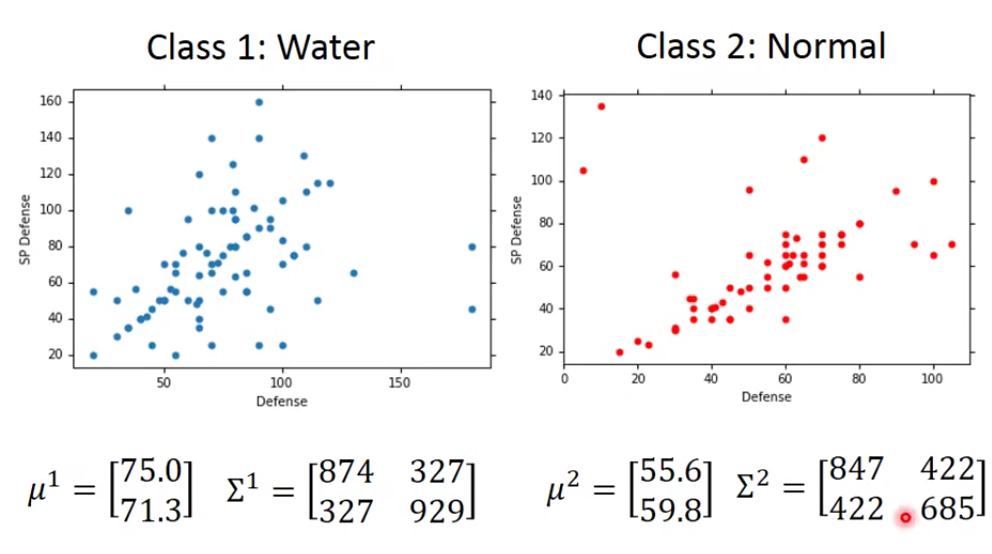
有了这些以后，我们可以得到这四个值，就可以开始做分类的问题了!

5.Do Classification

按照上面的方法我们真的去做一下，得到的结果是，我们发现它在二维空间看起来是重叠的，但是在7维空间可以分开，但是…

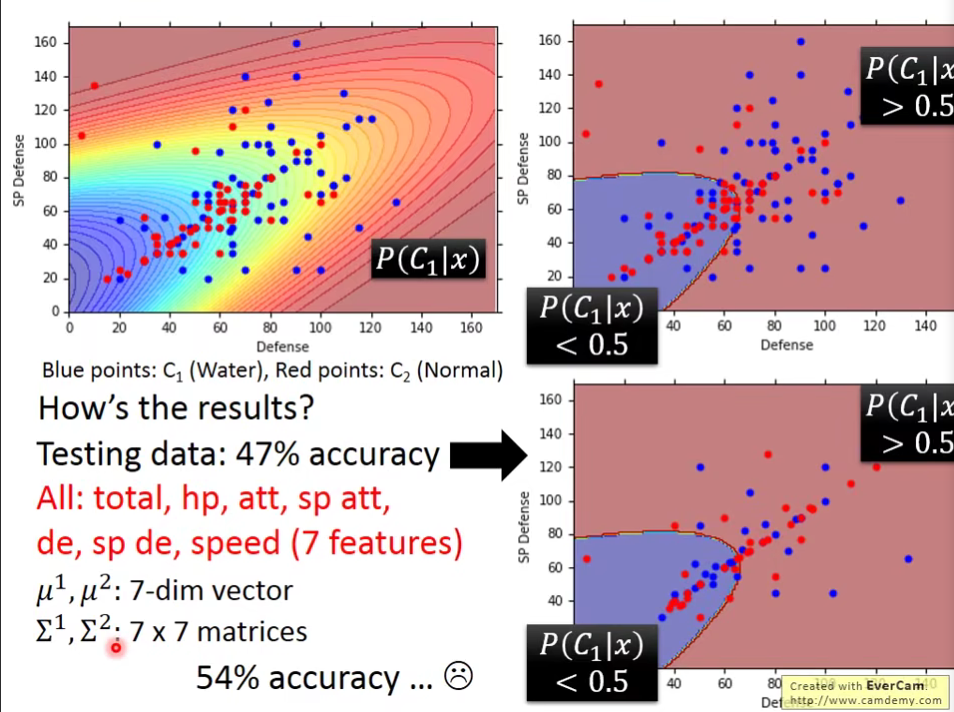
发现结果并不好😔，我们想办法改进它。

6.Modifying Model

其实之前使用的model是不常见的，你是不会经常看到给每一个Gaussian都有自己的mean和covariance。

我们对模型进行改进，不要让每一个Gaussian有一个自己的和，而考虑让某些share the same，这样我们可以减少参数量。

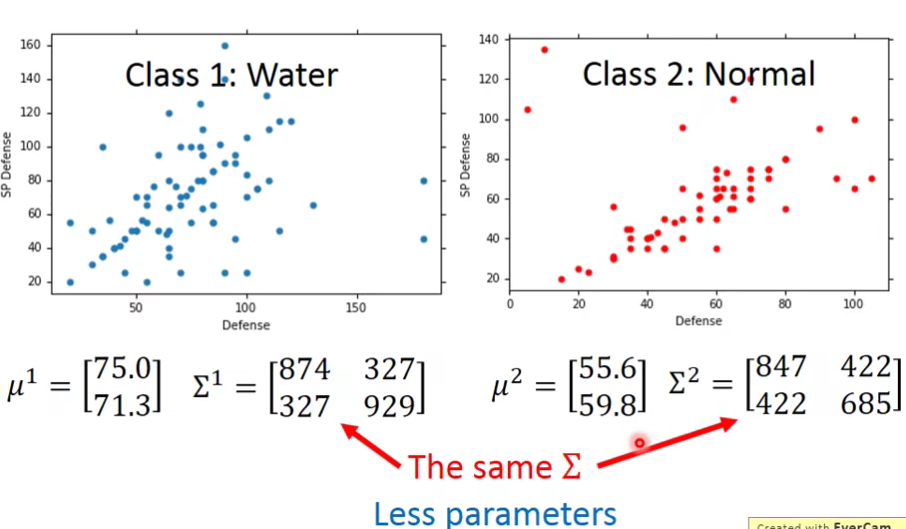
具体做法如下：

原先的等于和的加权和。

做完之后让我们看看效果：

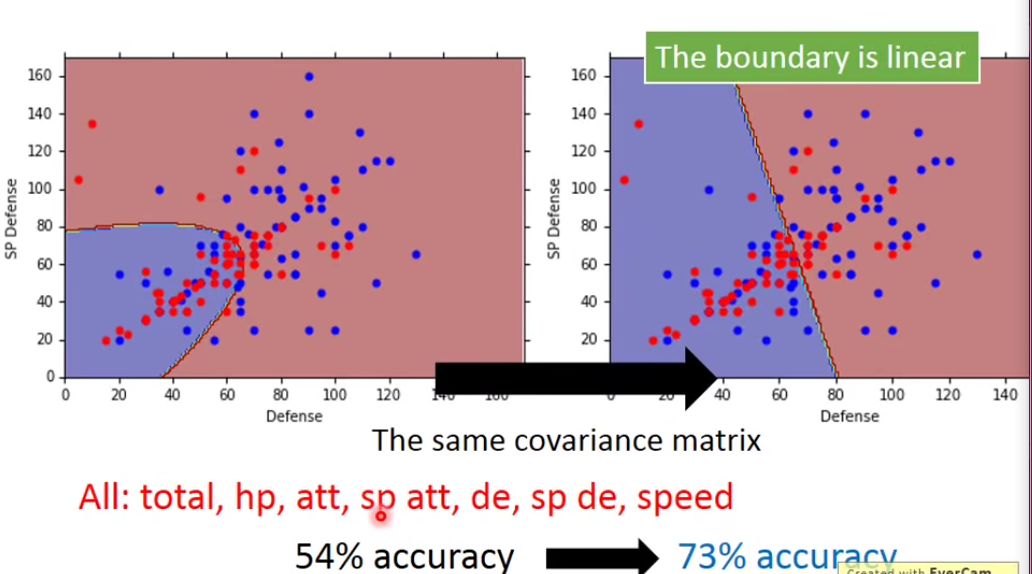
我们发现改成the same covariance matrix之后呢，the boundary is linear。我们称这种模型也是linear的。

为什么会这样子呢？为什么改成same covariance matrix 之后会变好呢？这个很难解释，因为它是在高维空间发生的事情，这也是Machine Learning它fancy的地方，人类没办法做的东西，机器可以帮我们做出来。

7.⭐Three Step of Classification

让我们来总结一下，如何去做分类问题。

Three Step

• Function Set(Model)
• Goodness of a function
• Find the best function:easy

而极大似然函数的输出值，就评价了这组参数的好坏

找到的那个最好的function，就是使值最大的那组参数，实际上就是所有样本点的均值和协方差。

这里上标i表示第i个点，这里x是一个features的vector，用下标来表示这个vector中的某个feature

8.Probability distribution

8.1 Why Gaussian distribution？

• You can always use the distribution you like 😉

其实这里只是拿高斯分布函数举一个例子而已，你当然可以选择自己喜欢的Probability distribution概率分布函数，如果你选择的是简单的分布函数(参数比较少)，那你的bias就大，variance就小；如果你选择复杂的分布函数，那你的bias就小，variance就大，那你就可以用data set来判断一下，用什么样的Probability distribution作为model是比较好的。

8.2 posterior probability(后验概率)

在贝叶斯统计 中，一个随机事件 或者一个不确定事件的后验概率（Posterior probability）是在考虑和给出相关证据或数据后所得到的条件概率 。同样，后验概率分布是一个未知量（视为随机变量 ）基于试验和调查后得到的概率分布。“后验”在本文中代表考虑了被测试事件的相关证据。

接下来我们来分析一下这个后置概率的表达式，会发现一些有趣的现象。

我们对model式子做一下变形。

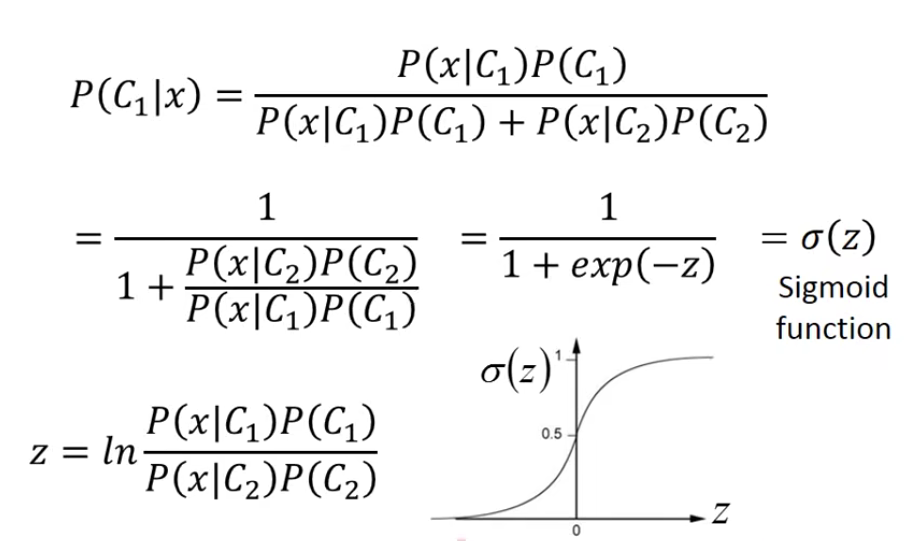
让我们来看看这个z到底长什么样子： 点击查看更多

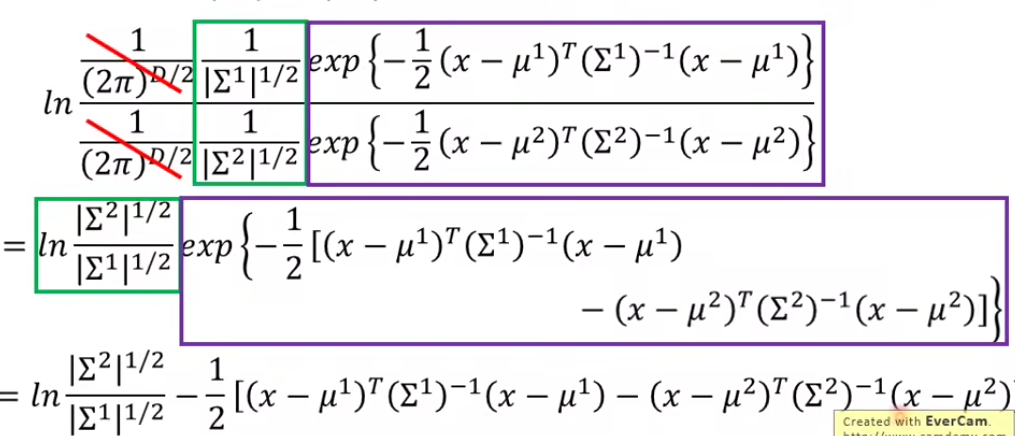
以上推导没看懂也没有关系，我们只需要知道经过一番推导，我们的z长这个样子：

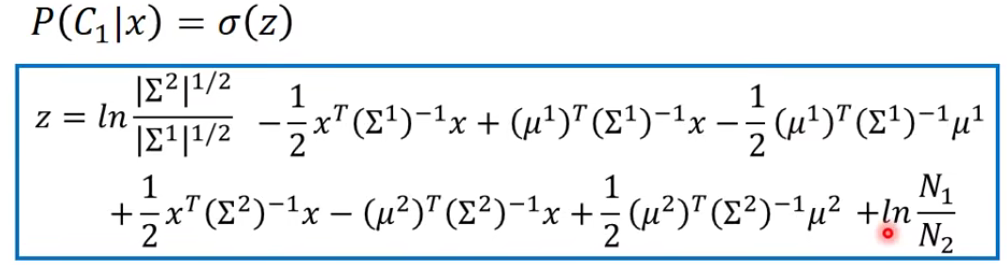
又因为我们上面说了convariance maxtrix(协方差矩阵) 是公用的，那么对上面式子进行简化：

化简出来相当于z=向量+常量

In generative model,we estimate ，then we have and 。

感觉很复杂,这里的w和x都是vector，两者的乘积是inner product，从上式中我们可以看出，现在这个model(function set)是受w和b控制的，因此我们为什么还要再去计算前面一大堆东西呢？

How about directly find and ?

下节继续…

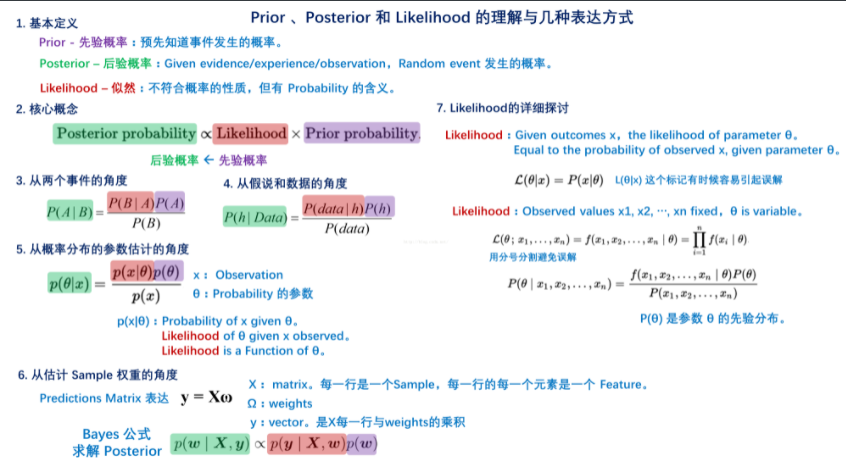
Prior、Posterior 和 Likelihood 的理解与几种表达方式： 点击查看更多