【从零开始的机器学习之旅】05-Logistic Regression(逻辑回归)
从零开始的机器学习之旅
1. Review
在classification这一章节,我们讨论了如何通过样本点的均值
进而利用
之后我们还推导了
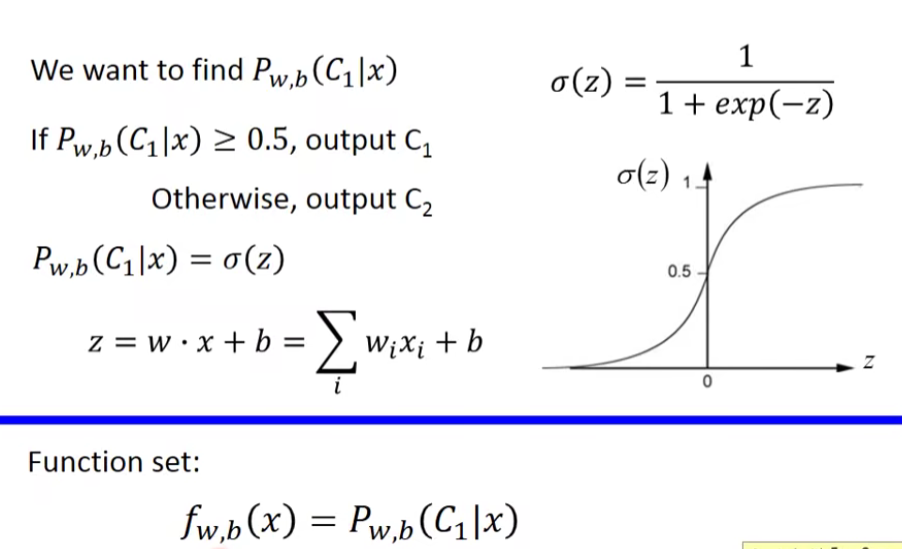
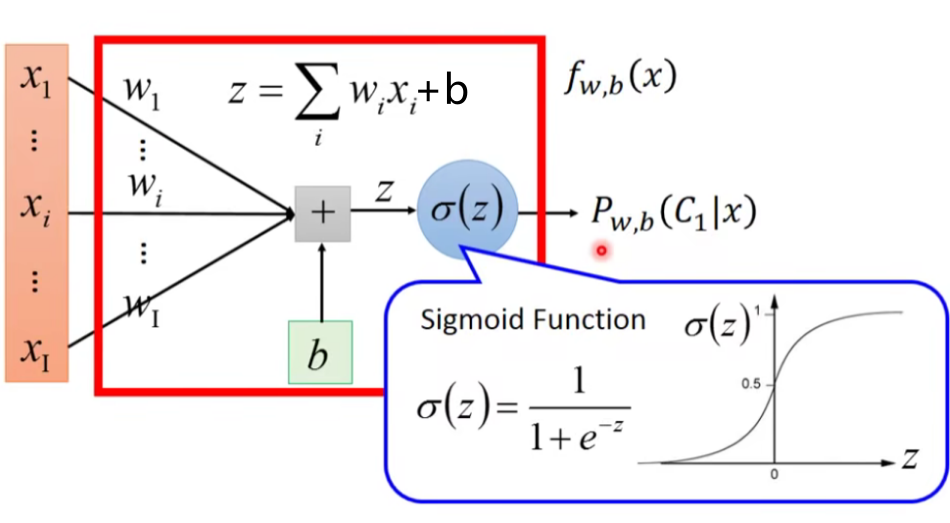
这里的w和x都是vector,两者的乘积是inner product,从上式中我们可以看出,现在这个model(function set)是受w和b控制的,因此我们不必要再去像前面一样计算一大堆东西,而是用这个全新的由w和b决定的model——Logistic Regression(逻辑回归)
2.Three Step of Machine Learning
2.2 Step2:Goodness of a Function

我们做一个数学上的转化:

于是: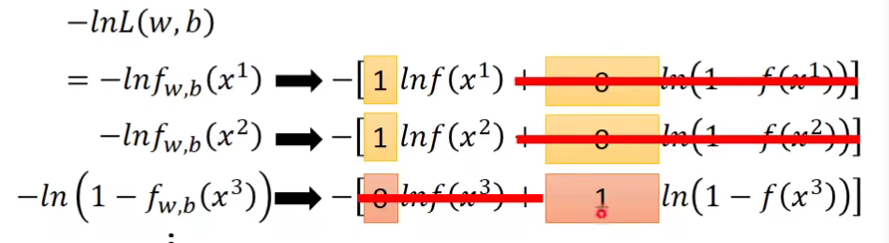
整理一下: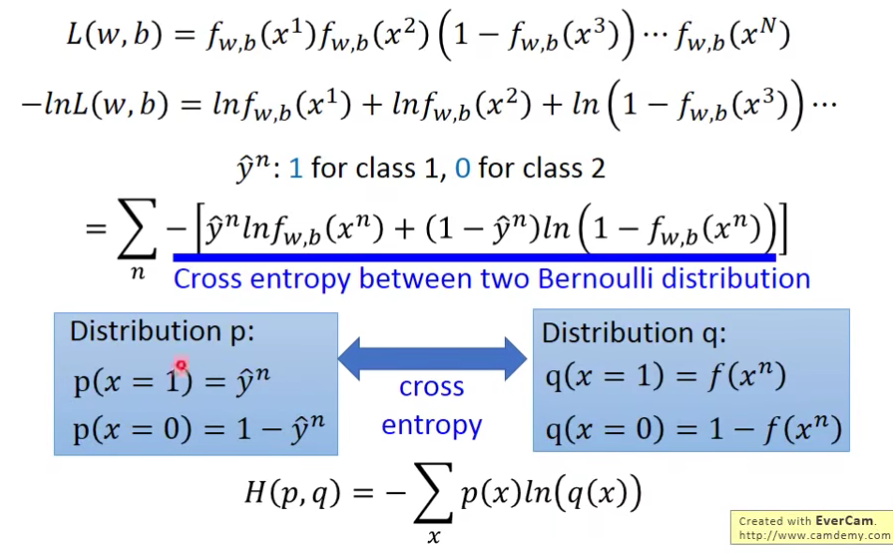
cross entropy(交叉熵): 点击查看更多
假设有上图两个distribution p和q,它们的交叉熵就是
cross entropy交叉熵的含义是表达这两个distribution有多接近,如果p和q这两个distribution一模一样的话,那它们算出来的cross entropy就是0。而这里的
总之,那么这里我们需要去minimize的就是:

即:
看这个那么复杂,你可能会有一个疑问:Why don’t we simply use square error as linear regression?
3.Logisitic Regression v.s. Linear Regression

4.Logistic Regression + Square error?
之前提到了,为什么Logistic Regression的loss function不能用square error来描述呢?我们现在来试一下这件事情,重新做一下machine learning的三个step

现在会遇到一个问题:如果第n个点的目标target是class 1,则
会变成0,这件事情是很合理的;但是当function的output
这会造成什么问题呢?
如果我们把参数的变化对total loss作图的话,loss function选择cross entropy或square error,参数的变化跟loss的变化情况可视化出来如下所示:(黑色的是cross entropy,红色的是square error)
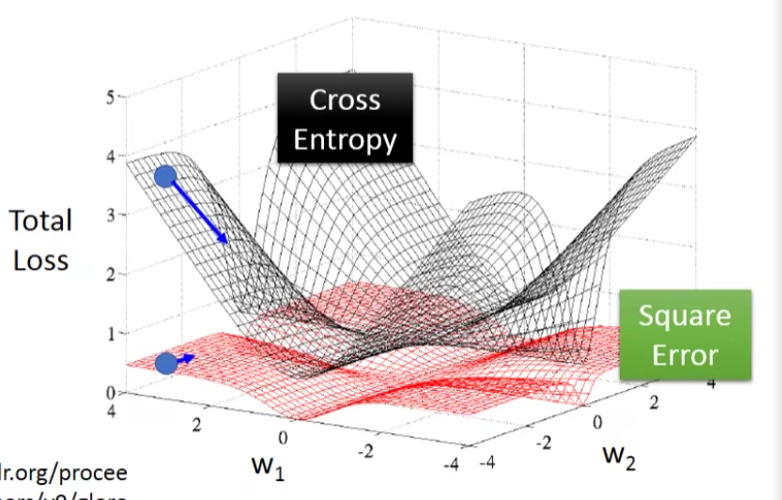
假设中心点就是距离目标很近的地方,如果是cross entropy的话,距离目标越远,微分值就越大,参数update的时候变化量就越大,迈出去的步伐也就越大,这是没问题的。
但当你选择square error的时候,过程就会很卡,因为距离目标远的时候,微分也是非常小的,移动的速度是非常慢的,我们之前提到过,实际操作的时候,当gradient接近于0的时候,其实就很有可能会停下来,因此使用square error很有可能在一开始的时候就卡住不动了,而且这里也不能随意地增大learning rate,因为在做gradient descent的时候,你的gradient接近于0,有可能离target很近也有可能很远,因此不知道learning rate应该设大还是设小。
综上,尽管square error可以使用,但是会出现update十分缓慢的现象,而使用cross entropy可以让你的Training更顺利。
5.Discriminative(判别模型) v.s. Generative(生成模型)
Logistic Regression的方法,我们把它称之为discriminative的方法;而我们用Gaussian来描述posterior Probability这件事,我们称之为Generative的方法。
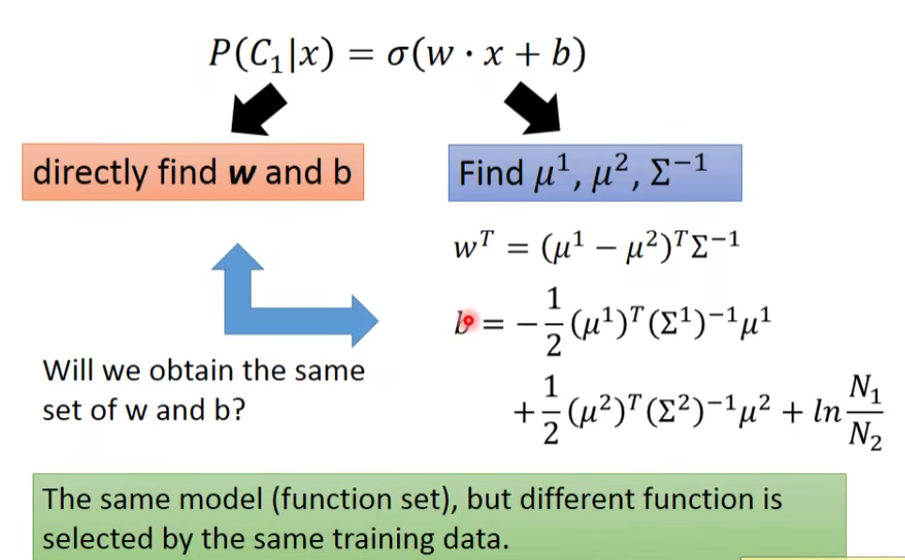
same model but different currency 。
什么意思呢?实际上它们用的model(function set)是一模一样的,都
你会发现用这两种方法得到的b和w是不同的,尽管我们的function set是同一个,但是由于做了不同的假设,最终从同样的Training data里找出来的参数会是不一样的。
在Logistic Regression里面,我们没有做任何实质性的假设,没有对Probability distribution有任何的描述,我们就是单纯地去找b和w(推导过程中的假设只是便于理解和计算,对实际结果没有影响)
而在Generative model里面,我们对Probability distribution是有实质性的假设的,之前我们假设的是Gaussian(高斯分布),甚至假设在相互独立的前提下是否可以是naive bayes(朴素贝叶斯),根据这些假设我们才找到最终的b和w
哪一个假设的结果是比较好的呢?Generative model和discriminative model的预测结果比较如下:
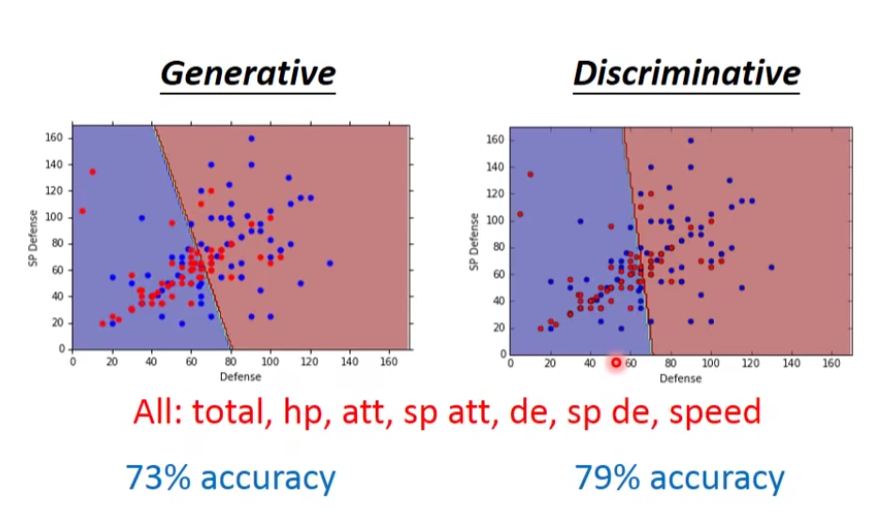
实际上Discriminative的方法常常会比Generative的方法表现得更好,这里举一个简单的例子来解释一下
5.1 toy example
假设总共有两个class,有这样的Training data:每一笔data有两个feature,总共有1+4+4+4=13笔data

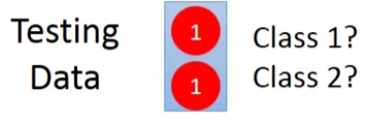
如果我们的testing data的两个feature都是1,凭直觉来说会认为它肯定是class 1,但是如果用**naive bayes的方法(朴素贝叶斯假设所有的feature相互独立,方便计算)**,得到的结果又是怎样的呢?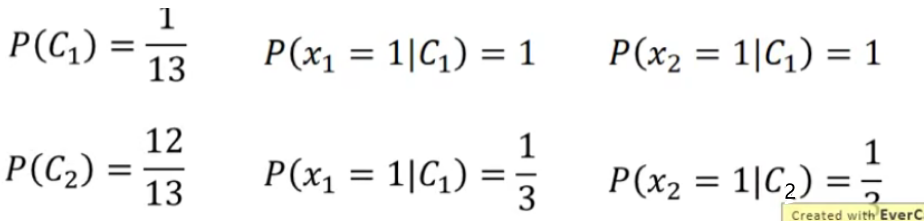
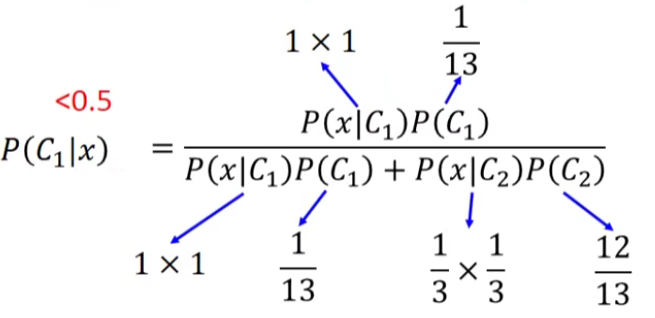
通过Naive bayes得到的结果竟然是这个测试点属于class 2的可能性更大,这跟我们的直觉比起来是相反的,实际上我们直觉认为两个feature都是1的测试点属于class 1的可能性更大是因为我们潜意识里认为这两个feature之间是存在某种联系的,但是对Naive bayes来说,它是不考虑不同dimension之间的correlation,Naive bayes认为在dimension相互独立的前提下,class 2没有sample出都是1的data,是因为sample的数量不够多,如果sample够多,它认为class 2观察到都是1的data的可能性会比class 1要大。
Naive bayes认为从class 2中找到样本点x的概率是x中第一个feature出现的概率与第二个feature出现的概率之积:
所以,Generative model和discriminative model的差别就在于,Generative的model它有做了某些假设,假设你的data来自于某个概率模型;而Discriminative的model是完全不作任何假设的。
Generative model做的事情就是脑补,它会自己去想象一些事情,于是会做出一个和我们人类直觉想法不太一样的判断结果,就像toy example里,我们做了naive bayes这样一个假设(事实上我们并不知道这两个feature是否相互独立),于是Naive bayes会在class 2里并没有出现过两个feature都是1的样本点的前提下,自己去脑补有这样的点。
那么脑补究竟是不是一件好的事情呢?
通常脑补不是一件好的事情,因为你给你的data强加了一些它并没有告诉你的属性,但是在data很少的情况下,脑补也是有用的,discriminative model并不是在所有的情况下都可以赢过Generative model,discriminative model是十分依赖于data的,当data数量不足或是data本身的label就有一些问题,那Generative model做一些脑补和假设,反而可以把data的不足或是有问题部分的影响给降到最低。
Benefit of generative model: 点击查看更多
- With the assumption of probability distribution,less training data is needed
- With the assumption of probability distribution more robust to the noise
- Priors and class-deoendent probabilities can be estimated from different sources.
在Generative model中,priors probabilities和class-dependent probabilities是可以拆开来考虑的,以语音辨识为例,现在用的都是neural network,是一个discriminative的方法,但事实上整个语音辨识的系统是一个Generative的system,它的prior probability是某一句话被说出来的几率,而想要estimate某一句话被说出来的几率并不需要有声音的data,可以去互联网上爬取大量文字,就可以计算出某一段文字出现的几率,并不需要声音的data,这个就是language model,而class-dependent的部分才需要声音和文字的配合,这样的处理可以把prior预测地更精确。
6.Conclusion
对于分类的问题(主要是二元分类),我们一般有两种方法去处理问题,一种是Generative的方法,另一种是Discriminative的方法,注意到分类问题的model都是从贝叶斯方程出发的,即
其中分子表示属于第i类的可能性,分母表示遍历从1到n所有的类的可能性。
两种方法的区别在于:
- Generative model会假设一个带参数的Probability distribution(概率分布),利用这个假设的概率分布函数带入(1)中去计算
- DIscriminative model不作任何假设,因此它无法通过假定的Probability distribution得到
- Generative model的好处是,它对data的依赖并没有像discriminative model那么严重,在data数量少或者data本身就存在noise的情况下受到的影响会更小,而它还可以做到Prior部分与class-dependent部分分开处理,如果可以借助其他方式提高Prior model的准确率,对整一个model是有所帮助的(比如前面提到的语音辨识)
- 而Discriminative model的好处是,在data充足的情况下,它训练出来的model的准确率一般是比Generative model要来的高的
7.Multi-class Classification(3 classes as example)
之前讲的都是二元分类的情况,这里讨论一下多元分类问题,其原理的推导过程与二元分类基本一致
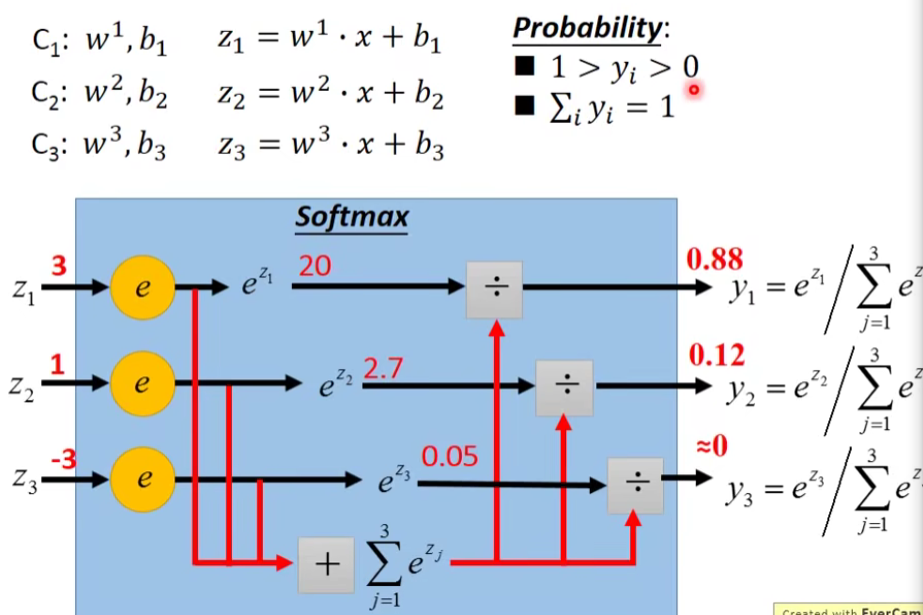
Softmax函数: 点击查看更多
Softmax函数是用于多类分类问题的激活函数,在多类分类问题中,超过两个类标签则需要类成员关系。对于长度为
Softmax函数与正常的max函数不同:max函数仅输出最大值,但Softmax函数确保较小的值具有较小的概率,并且不会直接丢弃。我们可以认为它是
Softmax激活函数的特点:
- 在零点不可微。
- 负输入的梯度为零,这意味着对于该区域的激活,权重不会在反向传播期间更新,因此会产生永不激活的死亡神经元。
multi-class classification的过程:
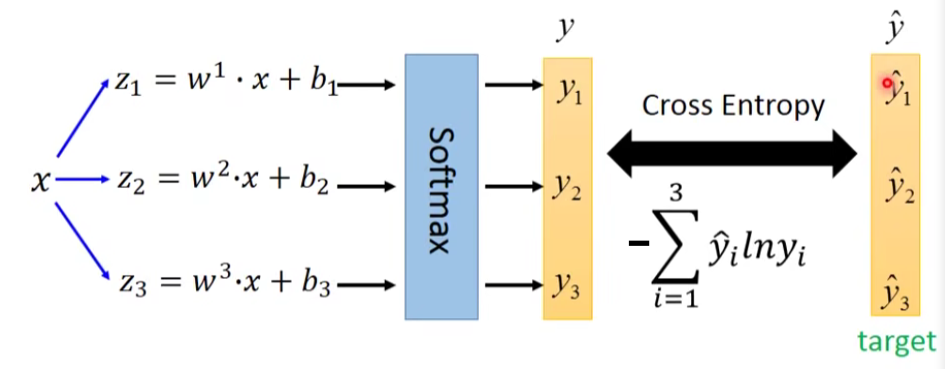
input x经过三个式子分别生成
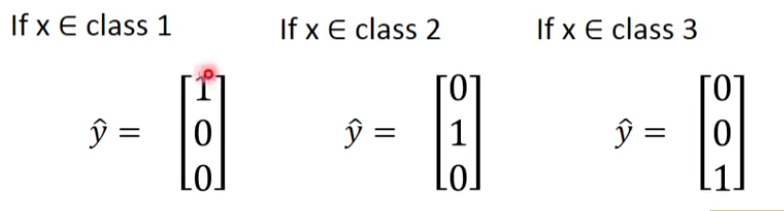
这个时候就可以计算一下output y和 target
8.Limitation of Logistic Regression
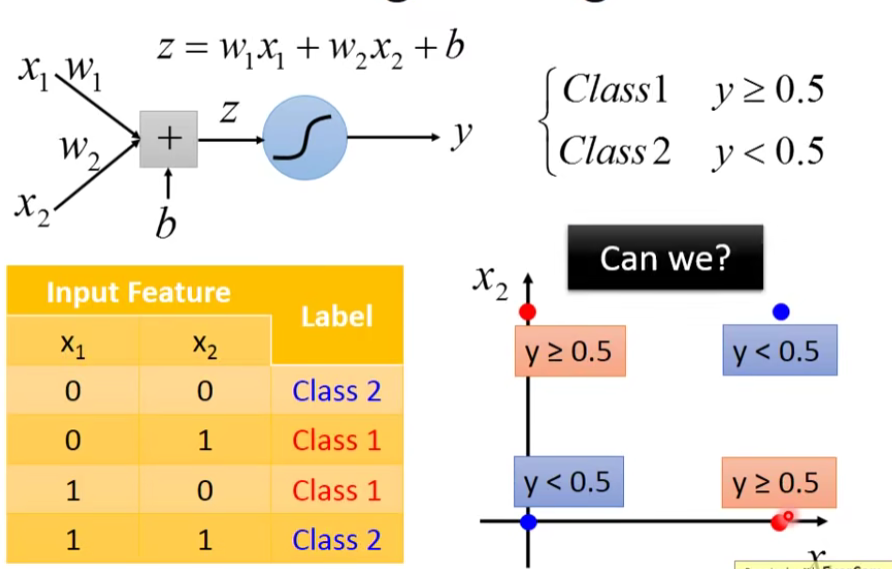
- No ,we can’t…☹
因为logistic regression的boundary就是一条直线,但是在这个平面上无论怎么画直线都不可能把图中的两个class分隔开来。
8.1Feature Transformation
如果你还是坚持要用Logistic Regression的话,有一招叫做Feature Transformation,原来的feature分布不好划分,那我们可以将之转化以后,找一个比较好的feature space,让Logistic Regression能够处理。
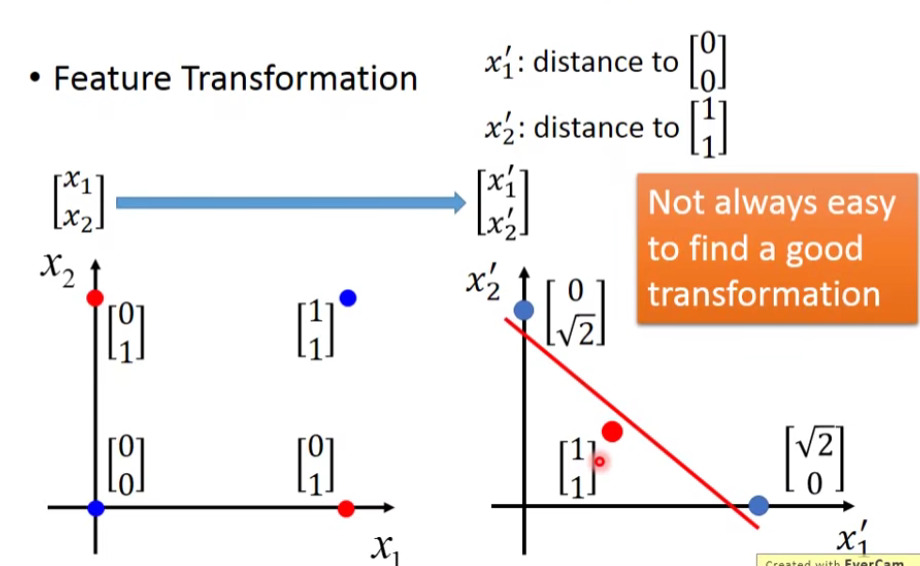
但麻烦的是,我们并不知道怎么做feature Transformation,如果在这上面花费太多的时间就得不偿失了,于是我们会希望这个Transformation是机器自己产生的,怎么让机器自己产生呢?我们可以让很多Logistic Regression cascade(连接)起来。
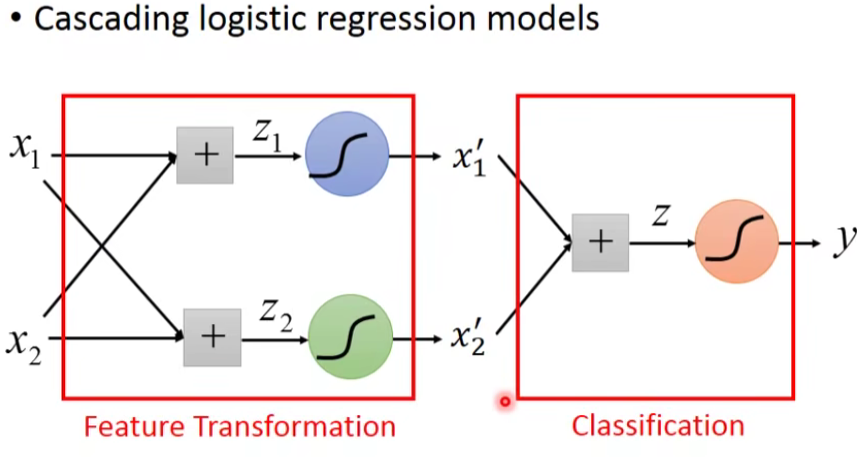
举个例子:
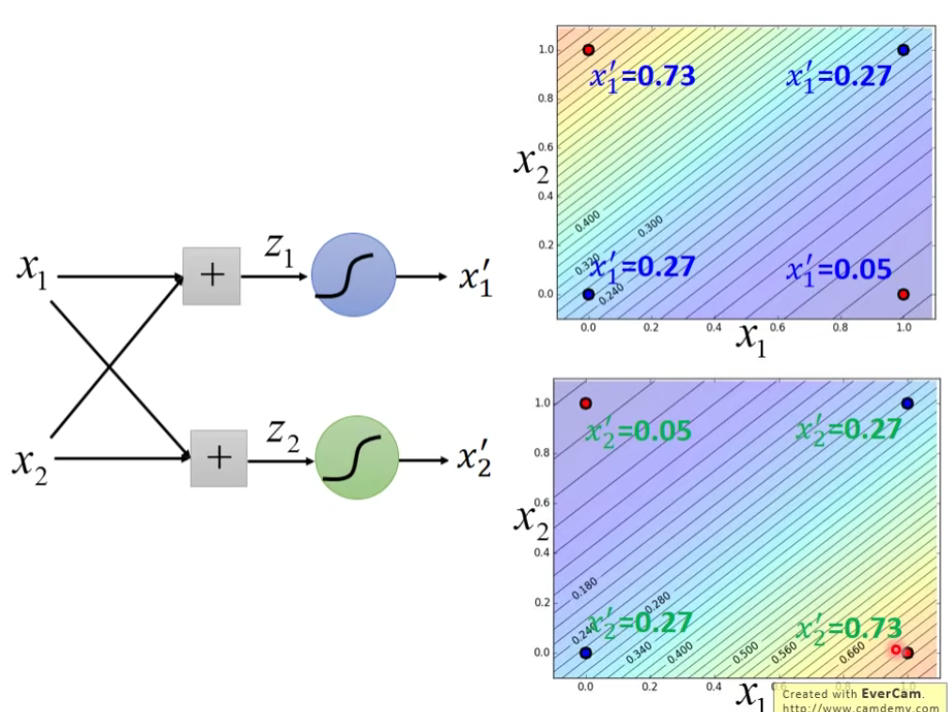
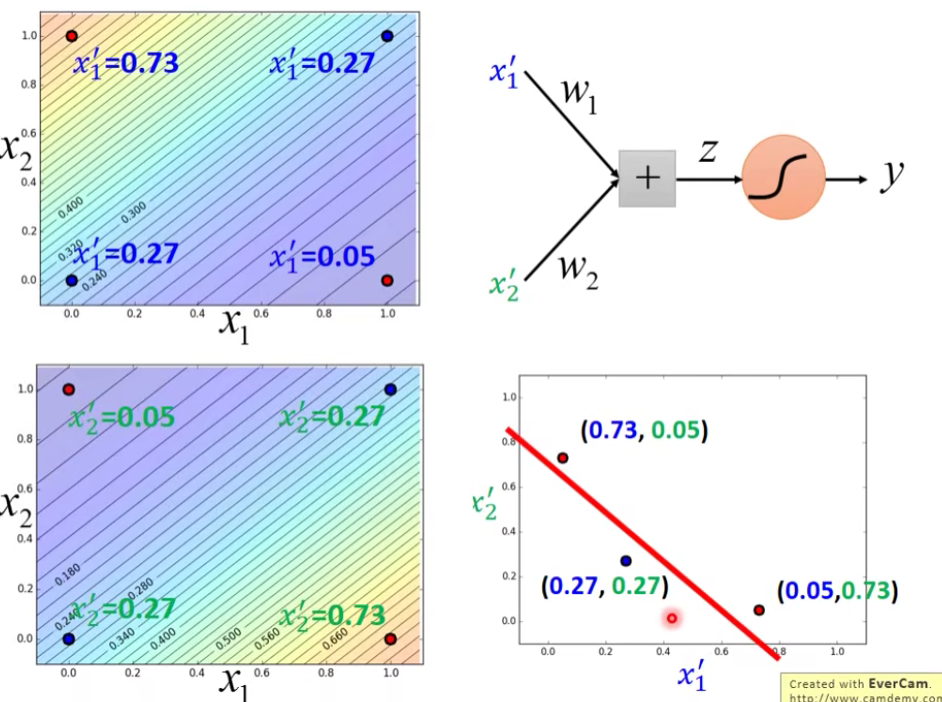
通过上面的例子,我们发现,多个Logistic Regression连接起来会产生powerful的效果,我们把每一个Logistic Regression叫做一个neuron(神经元),把这些Logistic Regression串起来所形成的network,就叫做Neural Network,就是类神经网路,这个东西就是Deep Learning!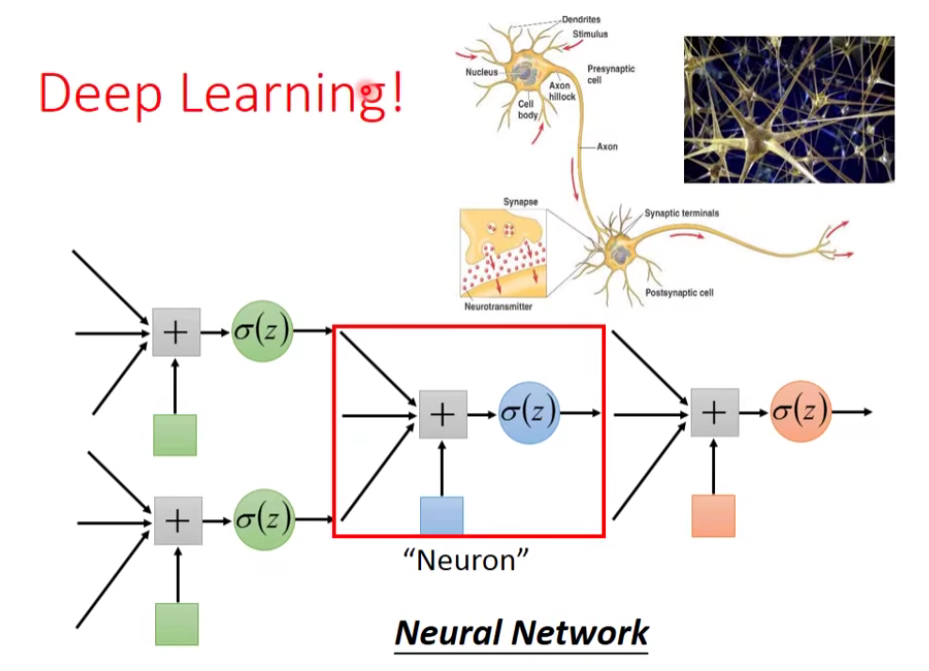
- Title: 【从零开始的机器学习之旅】05-Logistic Regression(逻辑回归)
- Author: Nannan
- Created at : 2024-07-01 01:19:12
- Updated at : 2024-09-29 23:21:07
- Link: https://redefine.ohevan.com/2024/07/01/05-Logistic Regression/
- License: This work is licensed under CC BY-NC-SA 4.0.