【从零开始的机器学习之旅】06-Convolutional Neural Network(CNN)
从零开始的机器学习之旅
——Network Architecture designed for Image
1.Image Classification
我们先来看一个例子:
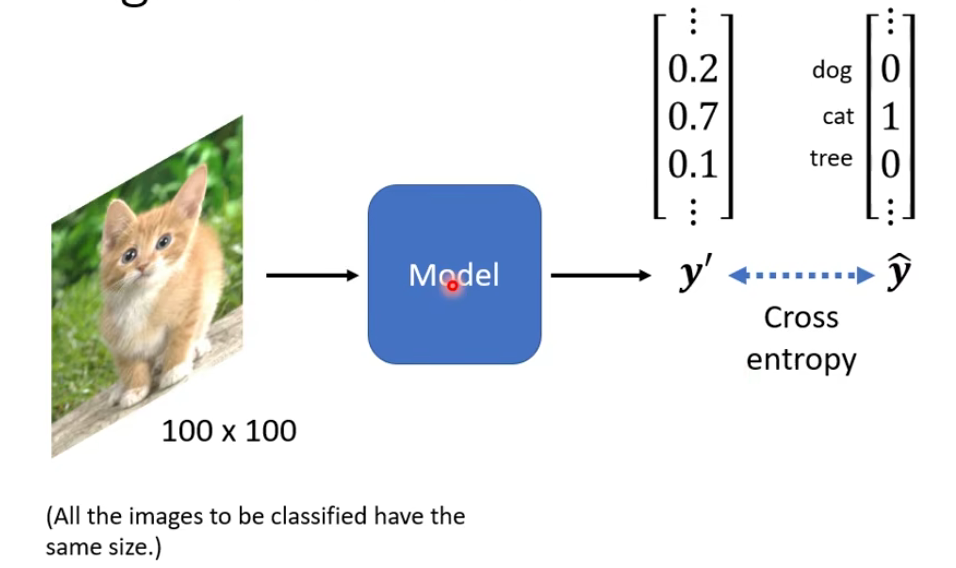
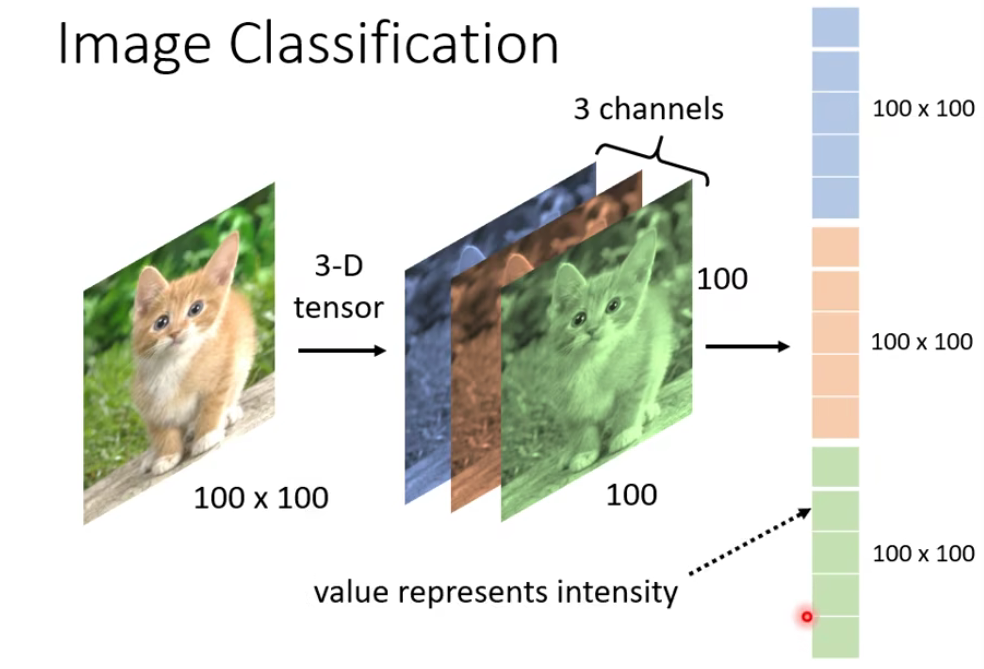
对machine来说,一张图片是长什么样子的呢?

我们把这三维拉直,变成一个向量,就可以当作network的输入啦。
那现在的问题是这样子:当我们直接用一般的fully connected的feedforward network来做图像处理的时候,往往会需要太多的参数。
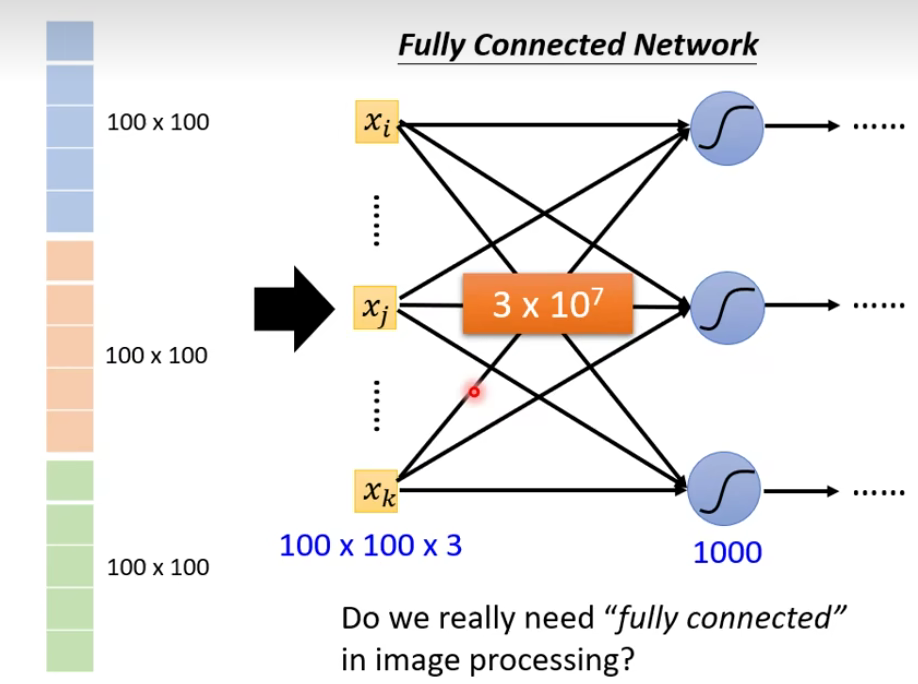
比如上述例子,假设这是一张
思考:Do we really need “fully connected” in image processing?
我们尝试对一张图进行观察:
1.1 Observation1
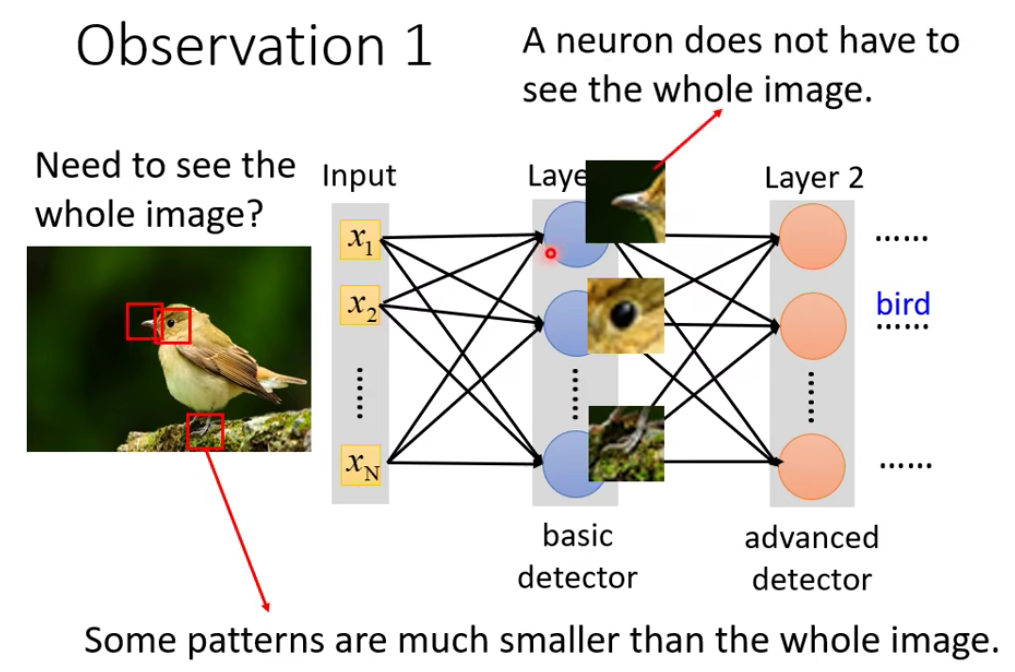
想想对于我们人来说,我们在判断一个物件的时候,往往也是抓最重要的特征。所以有些特征部位,其实我们不需要把一整张图作为输入,而只需要一小部分作为输入就行了。针对这个,我们可以做出简化。本来一个neuron要看一整张图片(fully connected),但是现在我们观察到有些其实不用给它看完整的图片,只需要给它看图片的一小部分就行了,那么我们要怎么去做呢?
在CNN里面,我们去设定这样一个区域,叫做Receptive field,对于某一个neuron来说,它只需要关注自己的field就行了。
1.2 Simplification1
——Receptive field

那么这个receptive field是要怎么决定出来呢?—— 取决于你的设定。
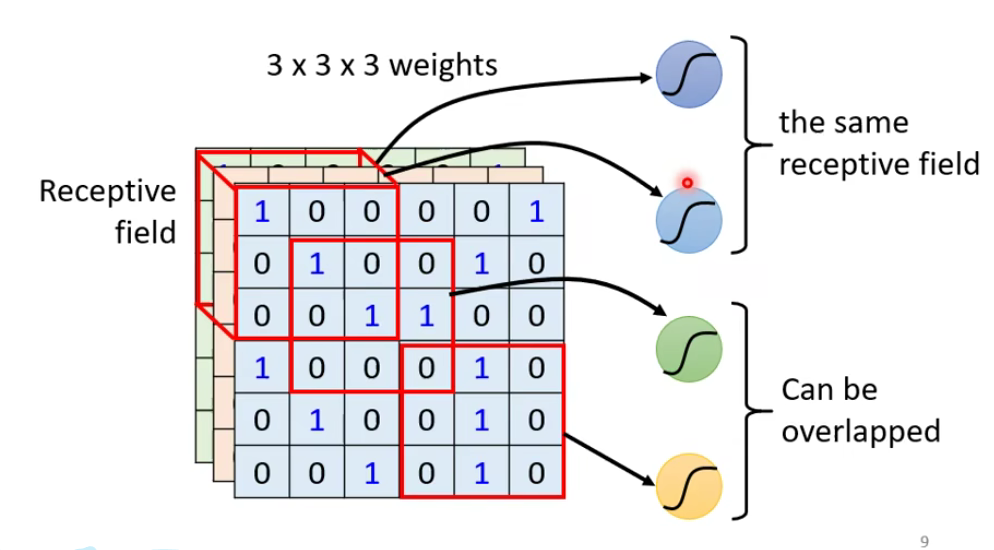
接下来你可能又会想:
- Can different neurons have different sizes of receptive field? yes
- Cover only some channels? yes
- Not square receptive field? yes
以上的想法都是可以的,但今天我们来讲一下最经典的一种
1.2.1 Typical Setting
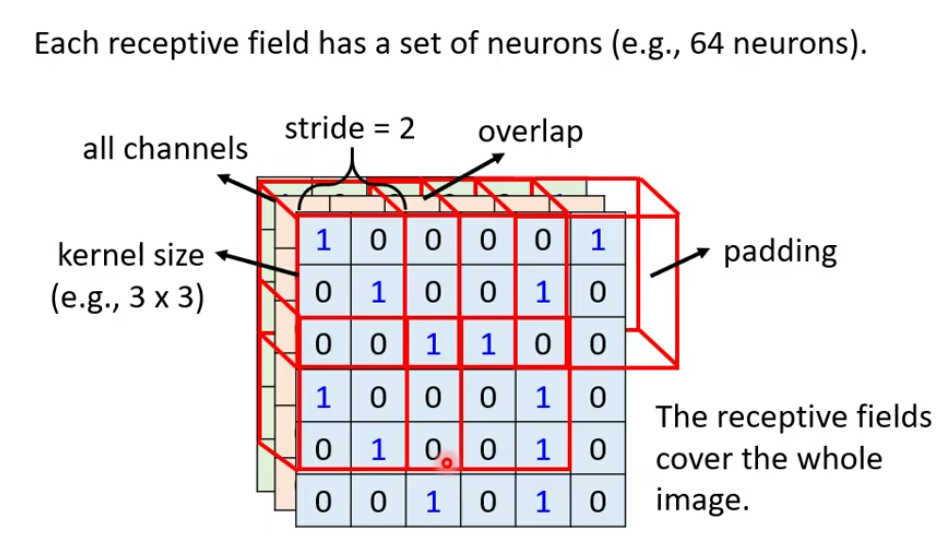
所以,CNN做的事情其实是,来简化这个neural network的架构,我们根据自己的知识和对图像处理的理解,一开始就把某些实际上用不到的参数给过滤掉,我们一开始就想一些办法,不要用fully connected network,而是用比较少的参数,来做图像处理这件事情。
⭐Filter(卷积核/过滤器)
filter是什么?什么是卷积?: 点击查看更多
在卷积神经网络中,卷积操作是指将一个可移动的小窗口(称为数据窗口,如下图绿色矩形)与图像进行逐元素相乘然后相加的操作。这个小窗口其实是一组固定的权重,它可以被看作是一个特定的滤波器(filter)或卷积核。这个操作的名称“卷积”,源自于这种元素级相乘和求和的过程。这一操作是卷积神经网络名字的来源。

上图这个绿色小窗就是数据窗口。简而言之,卷积操作就是用一个可移动的小窗口来提取图像中的特征,这个小窗口包含了一组特定的权重,通过与图像的不同位置进行卷积操作,网络能够学习并捕捉到不同特征的信息。
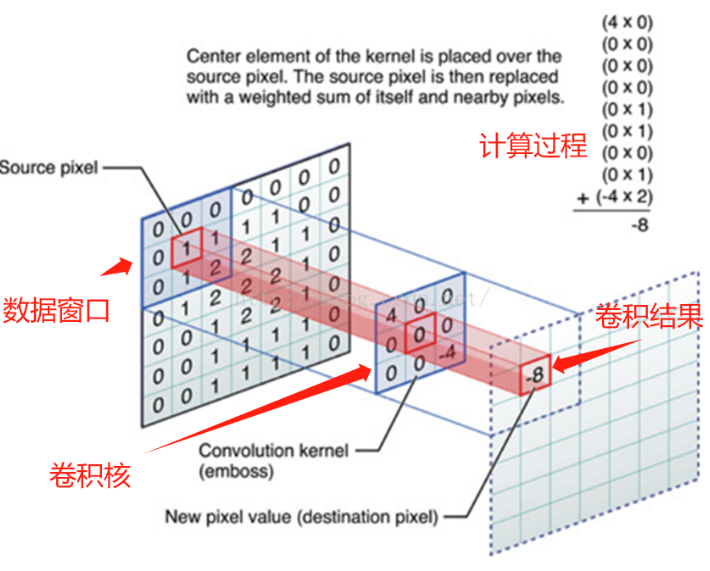
让我们来看动图直观一点:
这张图中蓝色的框就是指一个数据窗口,红色框为卷积核(滤波器),最后得到的绿色方形就是卷积的结果(数据窗口中的数据与卷积核逐个元素相乘再求和)
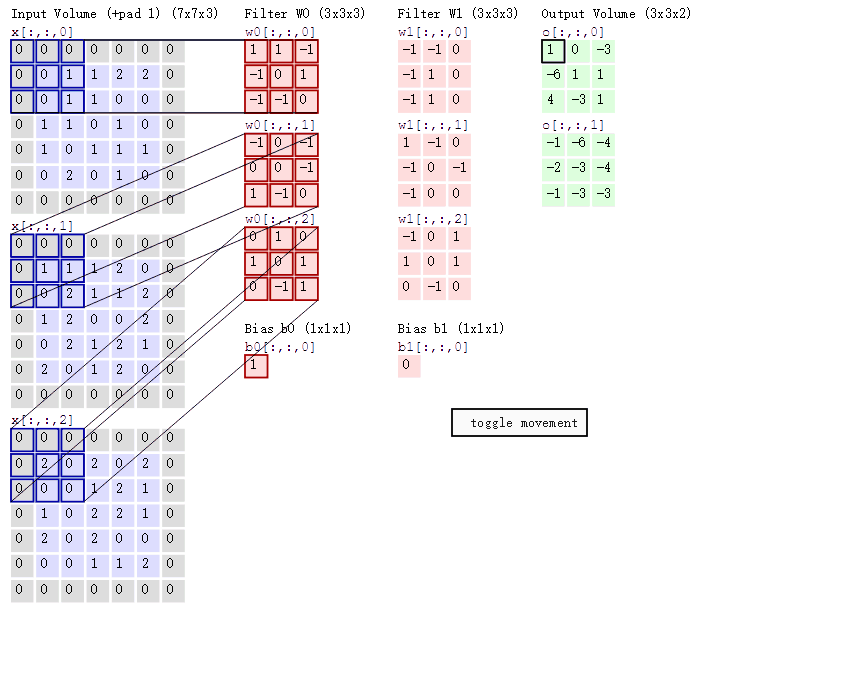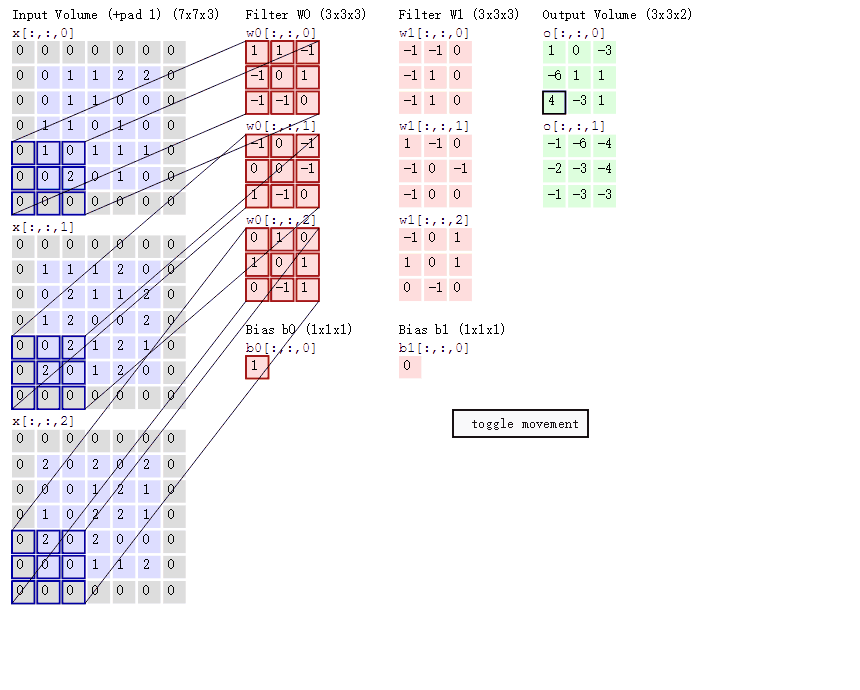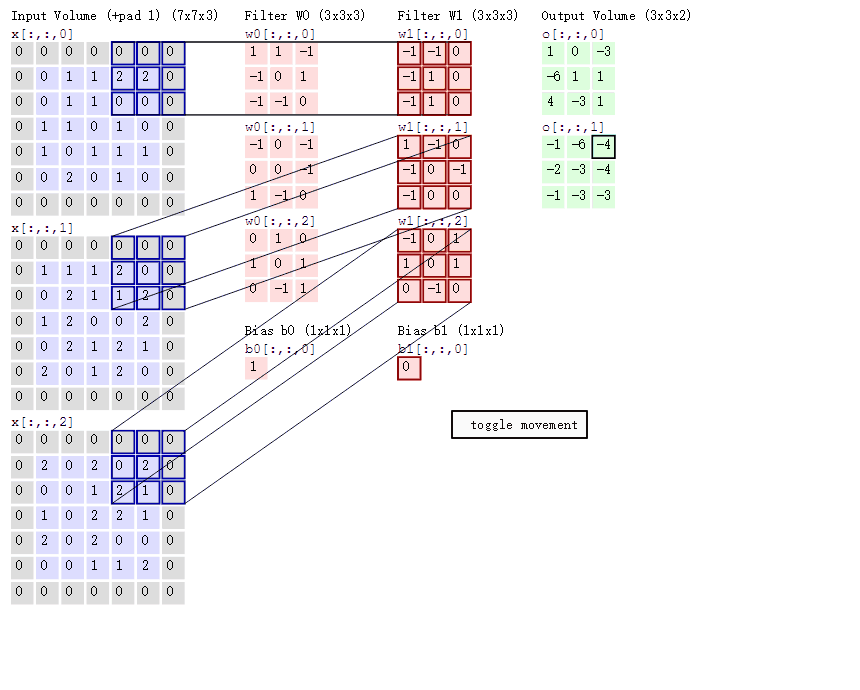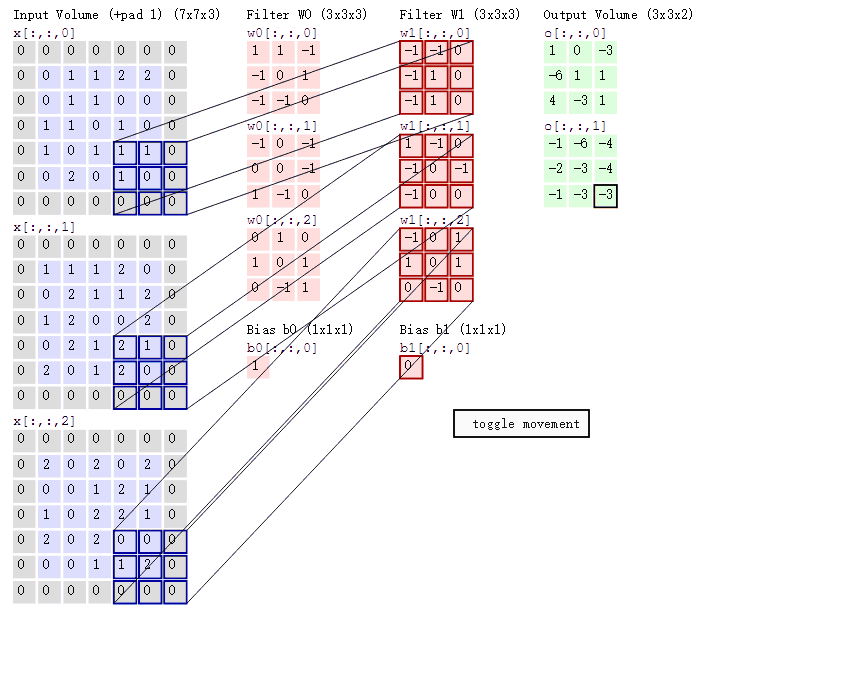
卷积的计算过程:
1.3 Overvation2
- The same patters appear in different regions.

我们发现它们做的事情是重复的,只是侦测的范围不一样,我们真的需要每个范围都去侦测吗?这样做太冗余了,我们要cost down(降低成本),我们并不需要有两个neuron、两组不同的参数来做duplicate(重复一样)的事情,所以我们可以要求这些功能几乎一致的neuron共用一组参数,它们share同一组参数就可以帮助减少总参数的量。
1.4 Simplification2
——parameter sharing
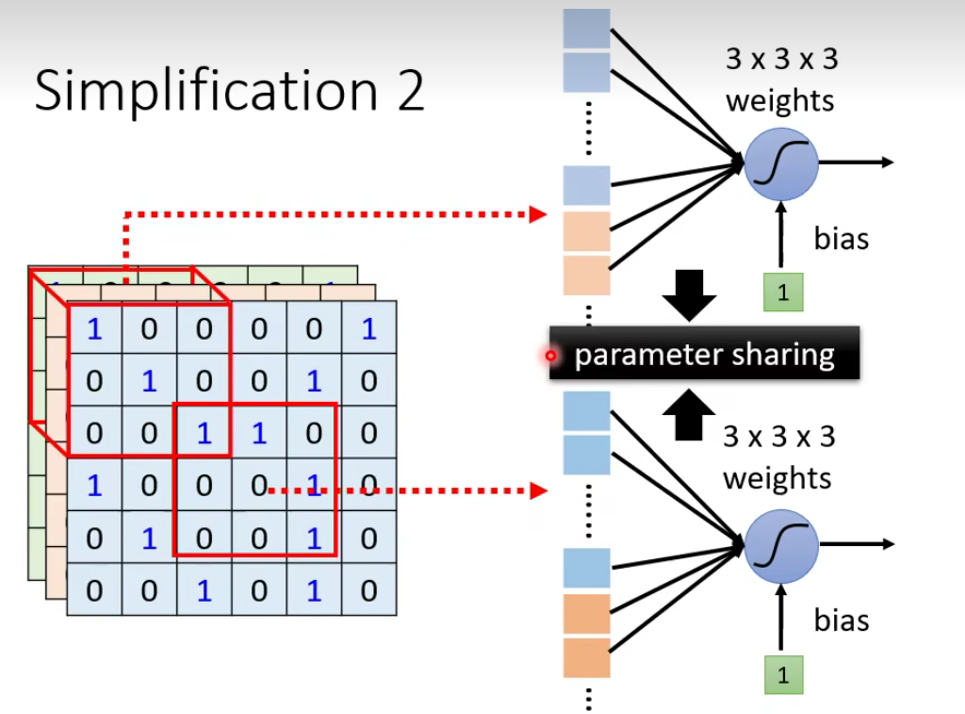
你可能又会思考一个问题,如果两个neuron共享参数,它们的输出会不会是一样的呢?虽然weight是一样的,但是input不一样,那么output可能不同。
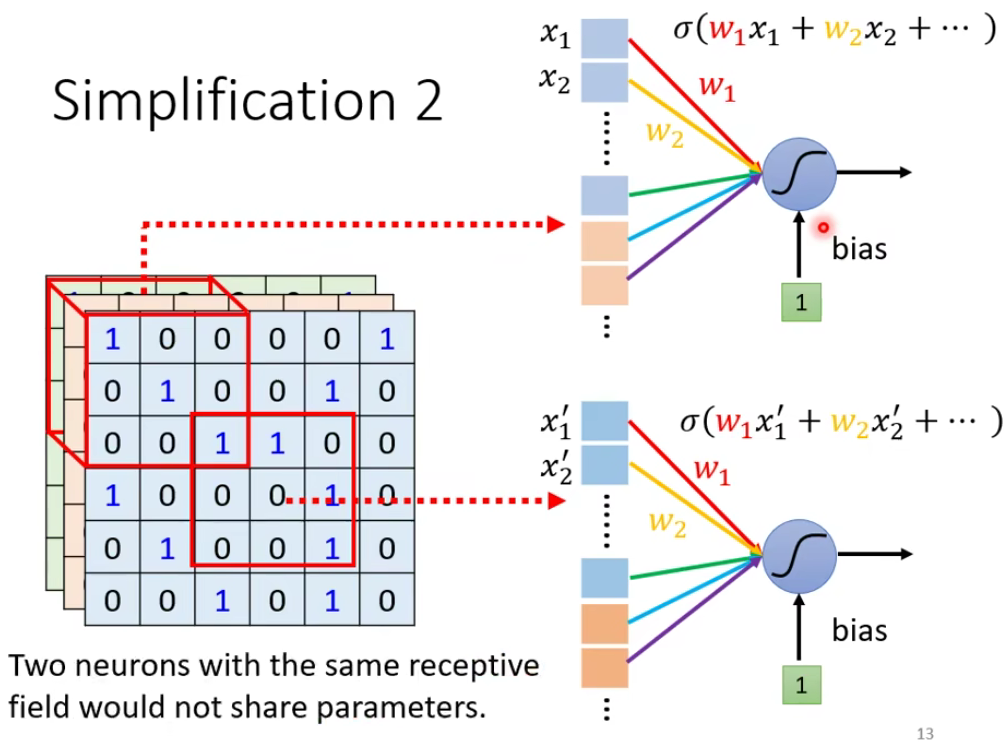
那么如何共享参数呢?这个也是由你自己决定的。下面来说一下常见的设定。
1.4.1 Typical Setting
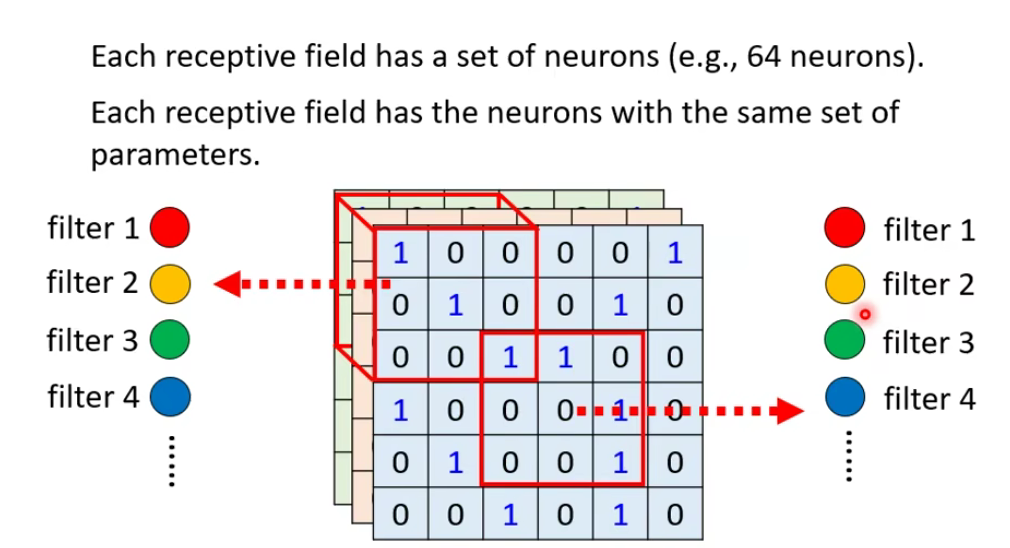
每个感受野都有一组神经元(例如,64 个神经元)。每个感受野都有具有相同参数集的神经元
1.5 Convolution v.s. Fully Connected
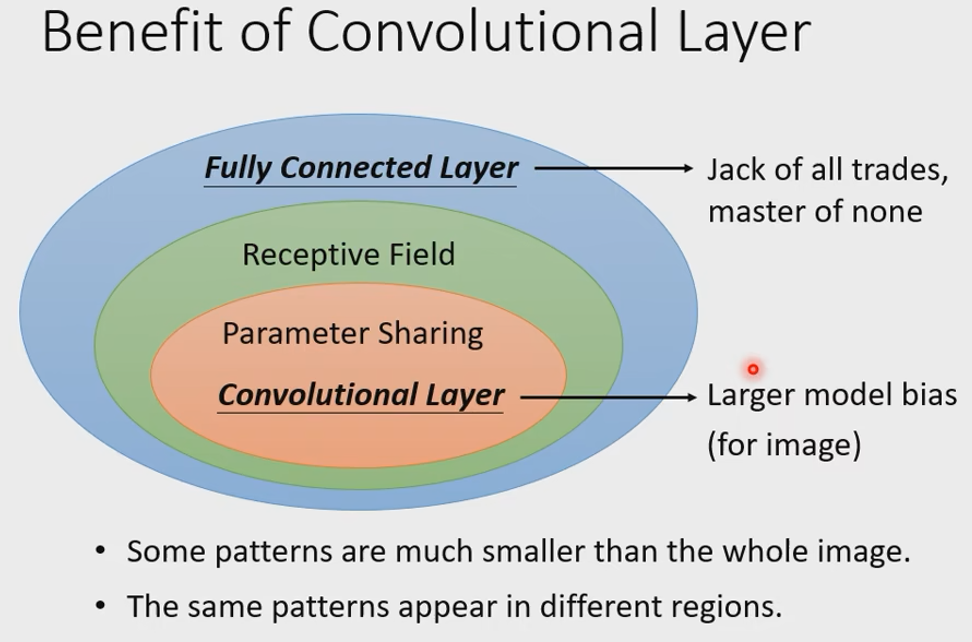
1.6 Another story based on filter
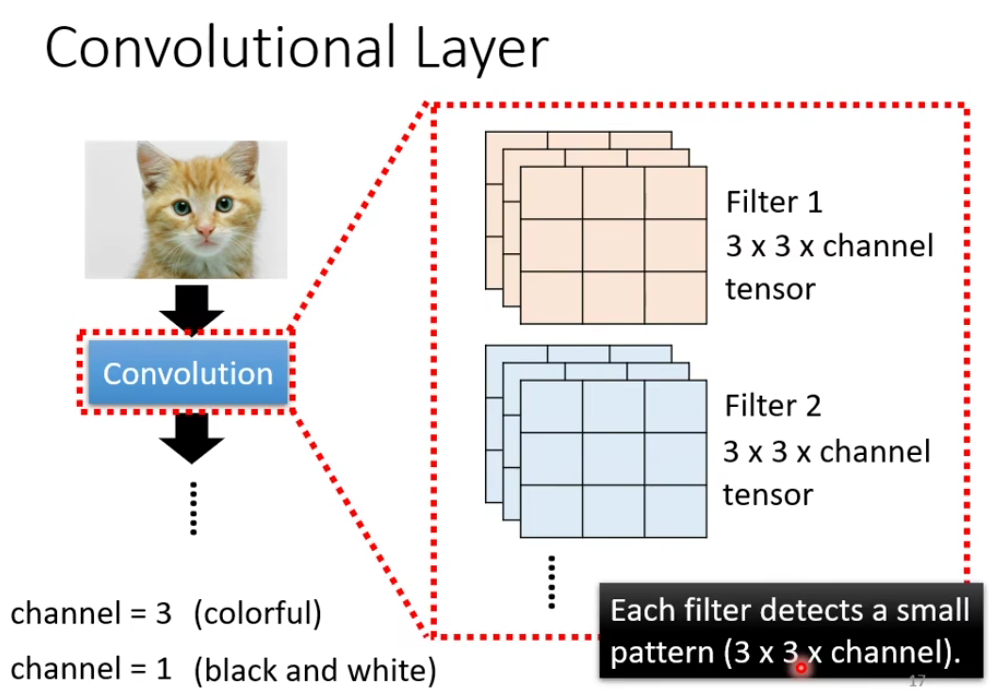
filter 是怎么从图片里面抓pattern的呢?我们举一个例子:
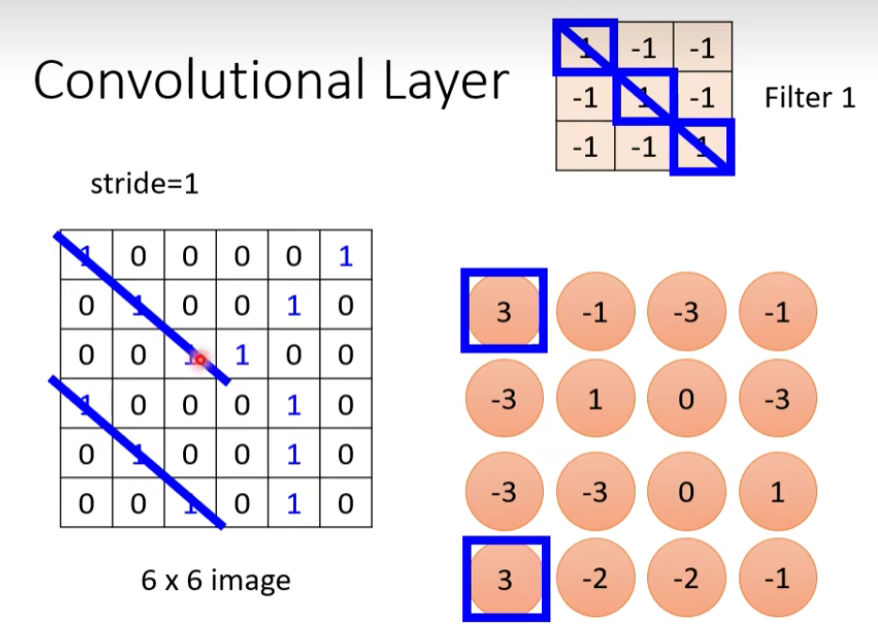
什么时候这个值最大呢?当斜着的3个1连起来的时候,那么说明左上角和左下角有出现这个patten。
然后继续做下一组filter,一直做直到做完这64组filter。
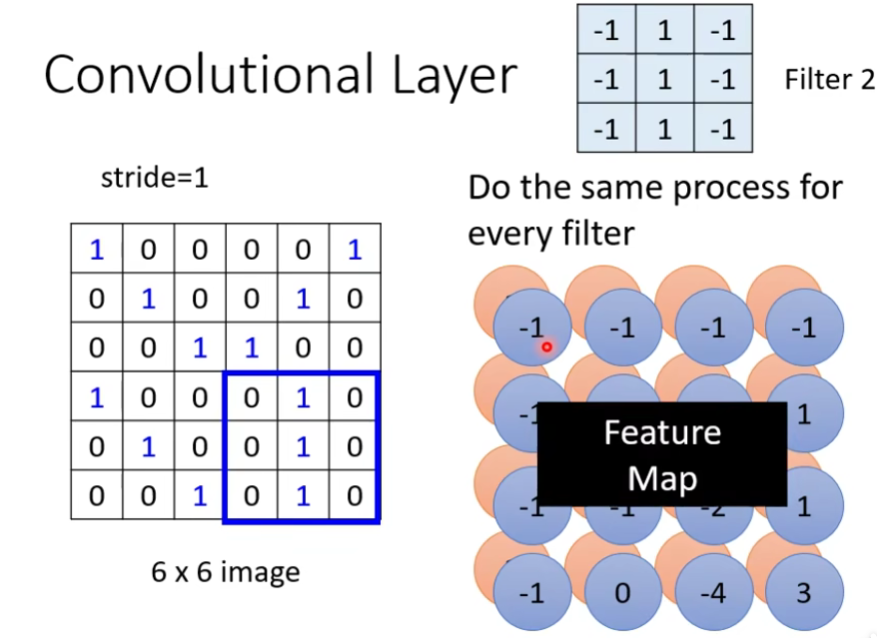
Feature Map
Feature Map 的理解: 点击查看更多
什么是Feature Map?
在cnn的每个卷积层,数据都是以三维形式存在的。你可以把它看成许多个二维图片叠在一起,其中每一个称为一个feature map。
feather map 是怎么生成的?
输入层:在输入层,如果是灰度图片,那就只有一个feature map;如果是彩色图片,一般就是3个feature map(红绿蓝)。
其它层:层与层之间会有若干个卷积核(kernel)(也称为过滤器),上一层每个feature map跟每个卷积核做卷积,都会产生下一层的一个feature map,有N个卷积核,下层就会产生N个feather map。
我们尝试叠多层:
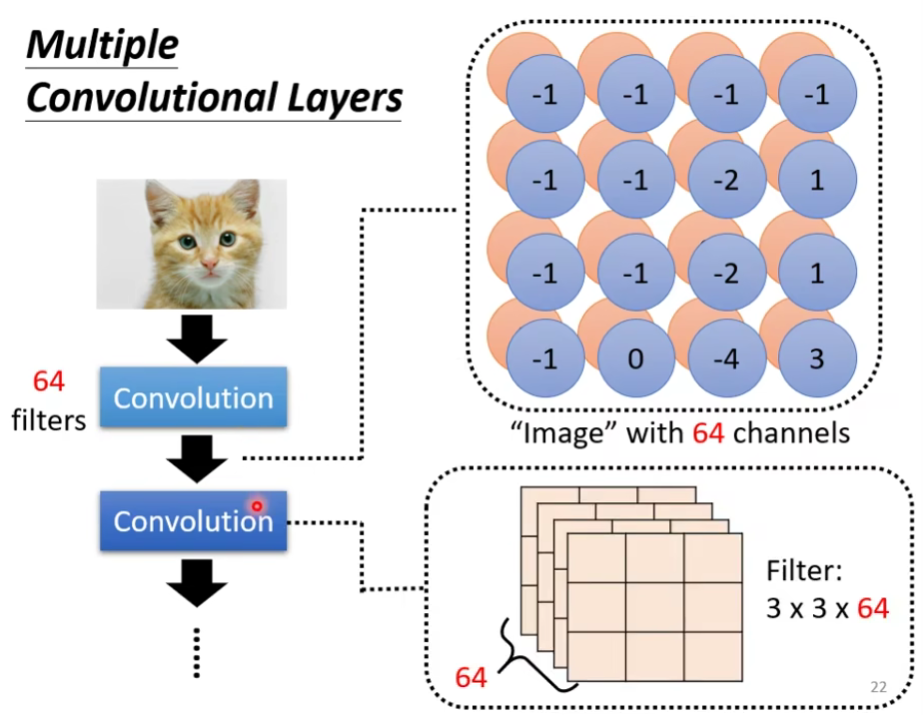
有一个问题:如果我们的filter的大小一直设
其实是不会的。我们在feature map上看到
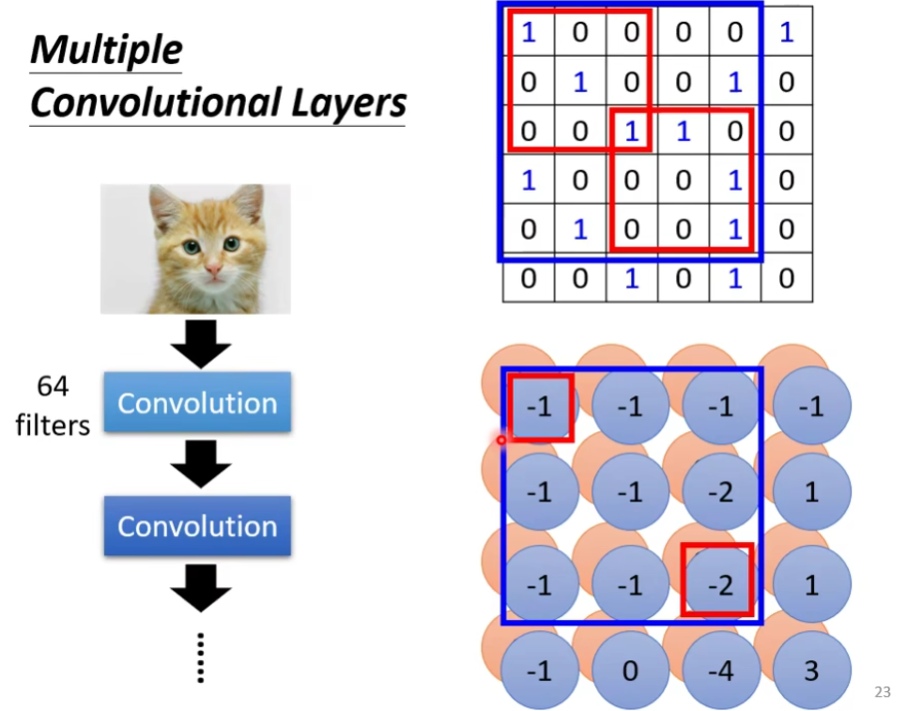
1.6.1 Comparison of Two Stories
Neuron Version Story
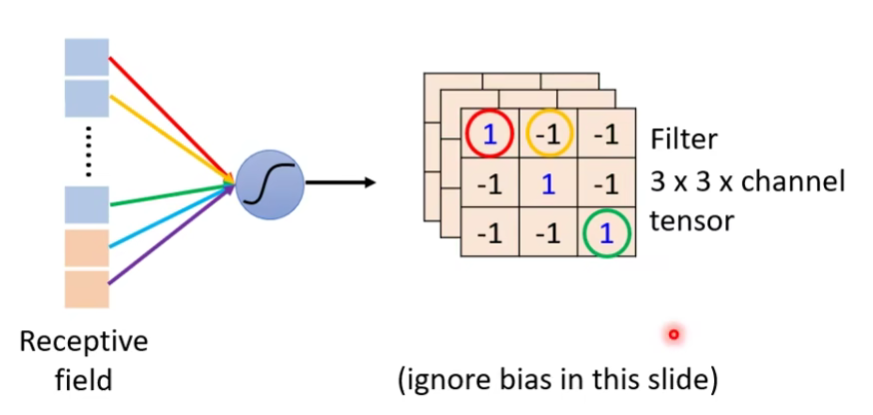
Filter Version Story
把filter扫过一张图其实就是convolution。
把filter扫过图片这件事情
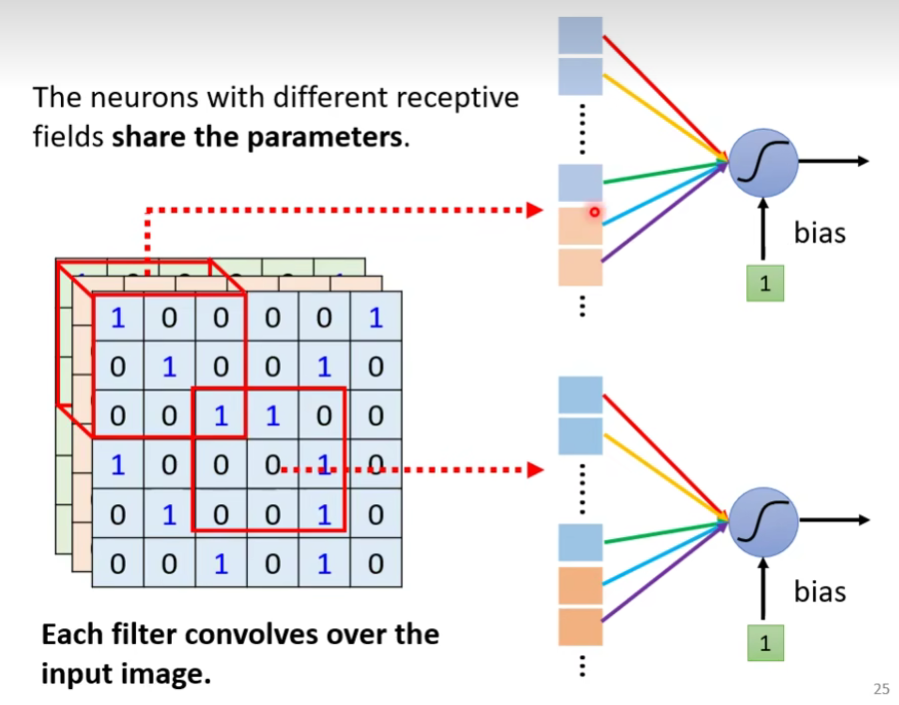
第一个版本的共用参数其实就是第二个版本里面的filter。
总而言之:

1.7 Observation3
- Subsampling the pixels will not change the object
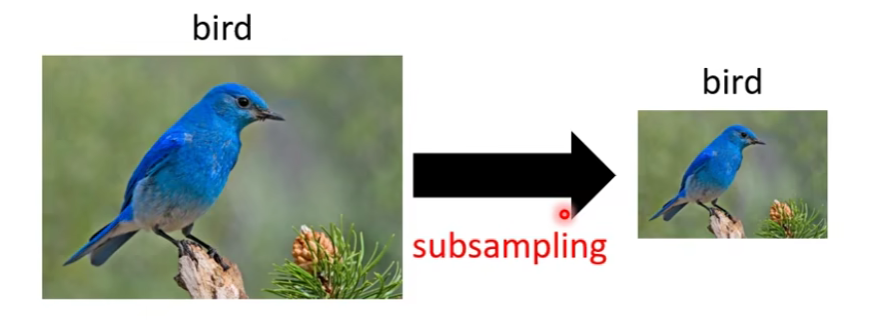
1.7.1 Pooling(池化) - Max Pooling
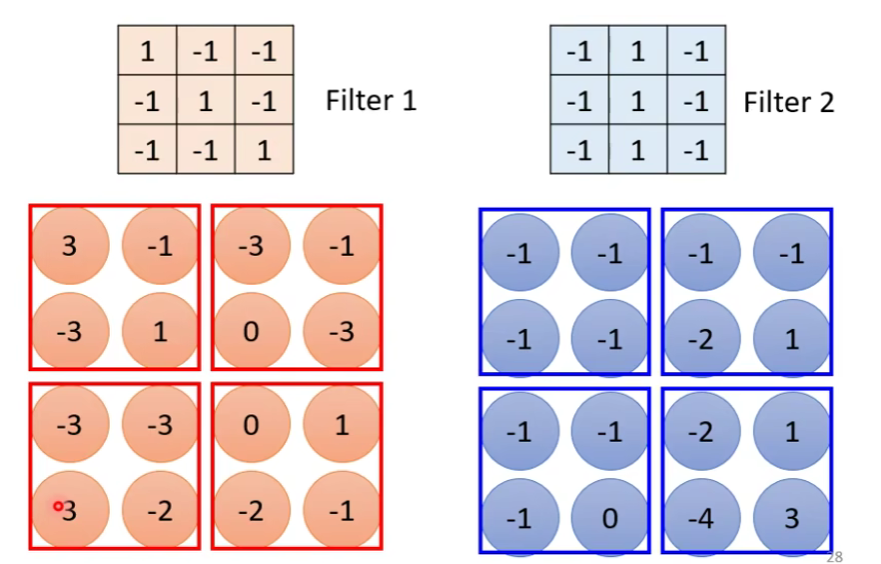
我们在每一组选一个代表(最大的那个Max Pooling)
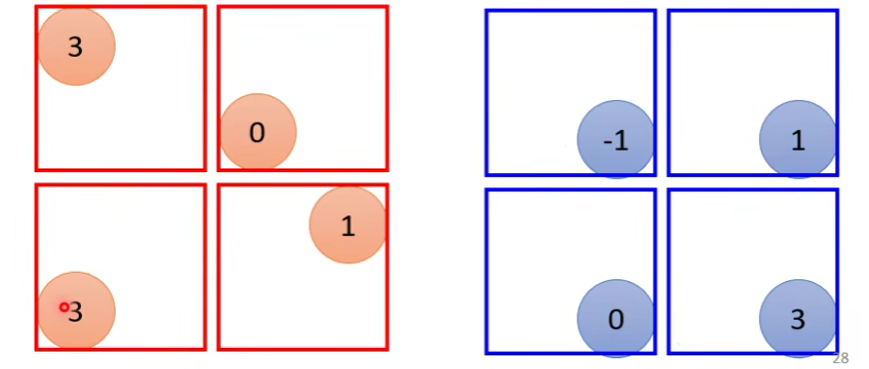
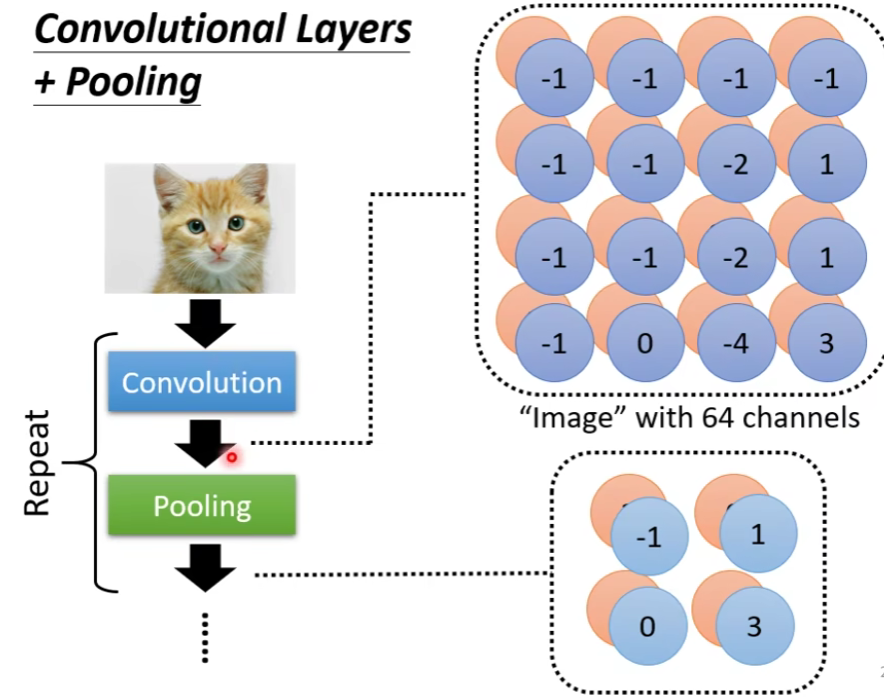
1.7.2 Convolutional Layers + Pooling(卷积层+池化)
做完一次convolution加一次max pooling,我们就把原来
所以,这是一个新的比较小的image,它表示的是不同区域上提取到的特征,实际上不同的filter检测的是该image同一区域上的不同特征属性,所以每一层channel(通道)代表的是一种属性,一块区域有几种不同的属性,就有几层不同的channel,对应的就会有几个不同的filter对其进行convolution操作。
当然,这件事情可以repeat很多次,你可以把得到的这个比较小的image,再次进行convolution和max pooling的操作,得到一个更小的image,依次类推…
2.⭐The whole CNN
2.1 Flatten(扁平化)
Flatten层的作用和应用: 点击查看更多
flatten层的作用是将多维的输入数据转化为一维的线性形式。具体来说,它通过将二维数组的各个元素逐个提取出来,形成一个连续的一维数组。例如,一个28x28的图像可以被展平为一个1维数组,长度为28*28=784。
在神经网络的训练和预测过程中,输入数据通常需要经过一系列的处理和转换。在图像分类任务中,输入的图片通常是一个二维数组,例如28x28像素的灰度图像。然而,神经网络的输入层通常需要一维的线性数组作为输入。这时,flatten层就派上了用场。
在实际应用中,flatten层通常位于卷积层之后。卷积层可以提取图像中的局部特征,而flatten层则将这些特征展平为一维形式,以便于全连接层的处理。在全连接层中,神经元会对一维的输入数据进行加权求和并计算激活值,从而完成分类或回归任务。
做完convolution和max pooling之后,就是FLatten和Fully connected Feedforward network的部分。
Flatten的意思是,把左边的feature map拉直**(多维的输入数据转化为一维的线性形式)**,然后把它丢进一个Fully connected Feedforward network,然后可能还要做个softmax,然后就结束了。
也就是说,我们之前通过CNN提取出了image的feature,它相较于原先一整个image的vetor,少了很大一部分内容,因此需要的参数也大幅度地减少了,但最终,也还是要丢到一个Fully connected的network中去做最后的分类工作。
2.2 卷积神经网络的构造
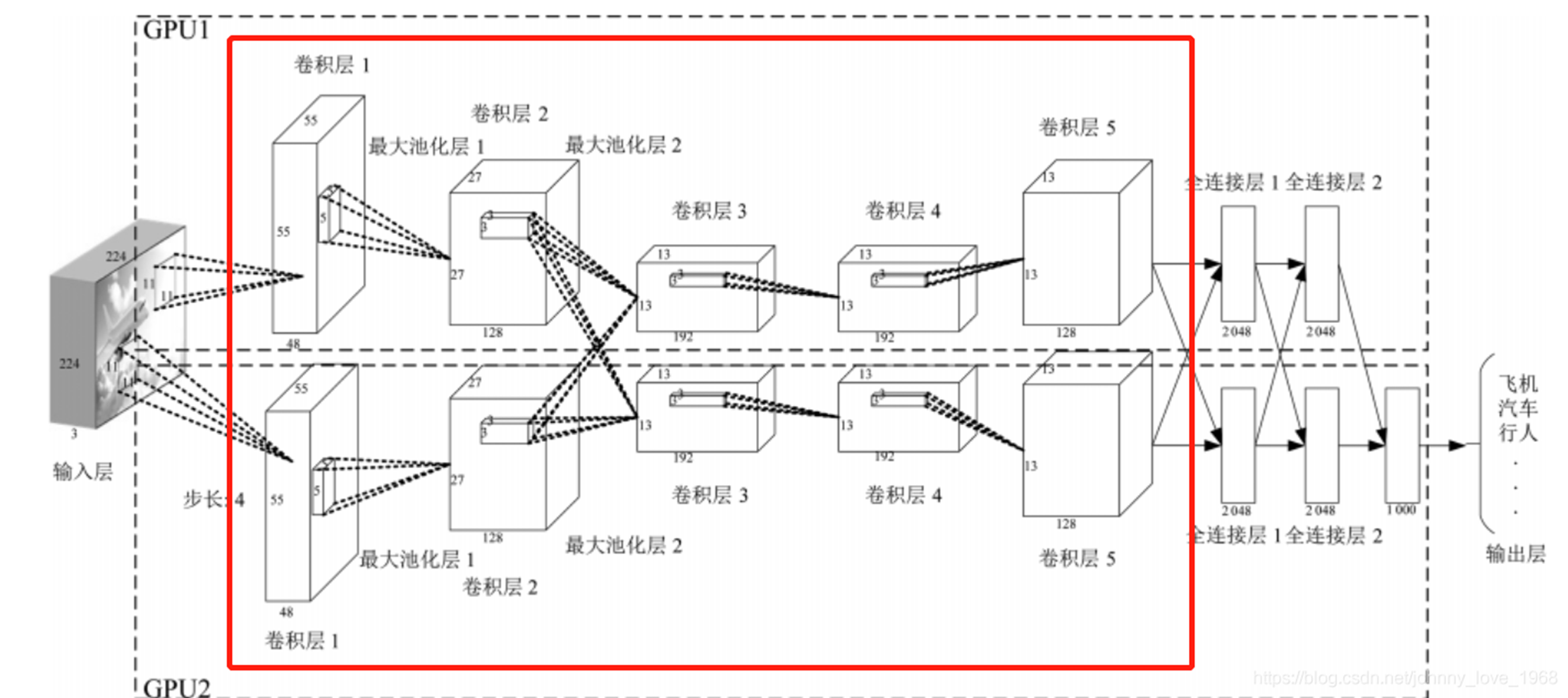
输入层
输入层接收原始图像数据。图像通常由三个颜色通道(红、绿、蓝)组成,形成一个二维矩阵,表示像素的强度值。卷积和激活
卷积层将输入图像与卷积核进行卷积操作。然后,通过应用激活函数(如ReLU)来引入非线性。这一步使网络能够学习复杂的特征。池化层
池化层通过减小特征图的大小来减少计算复杂性。它通过选择池化窗口内的最大值或平均值来实现。这有助于提取最重要的特征。多层堆叠
CNN通常由多个卷积和池化层的堆叠组成,以逐渐提取更高级别的特征。深层次的特征可以表示更复杂的模式。全连接和输出
最后,全连接层将提取的特征映射转化为网络的最终输出。这可以是一个分类标签、回归值或其他任务的结果。
过程:
展开形式:
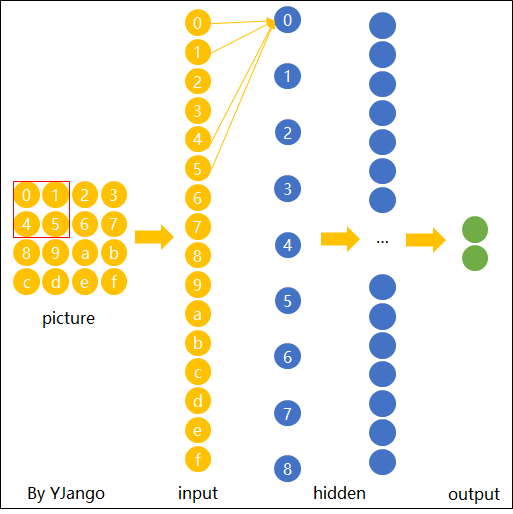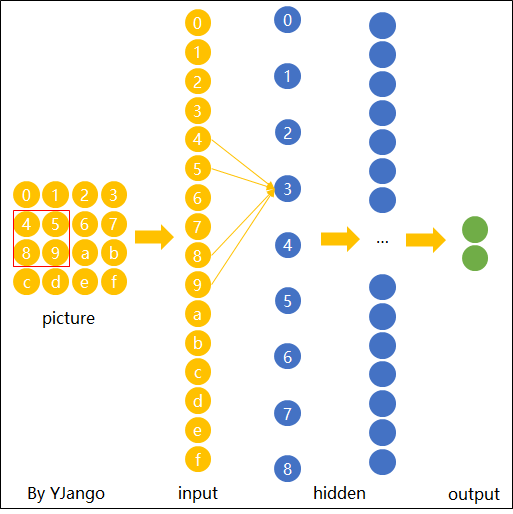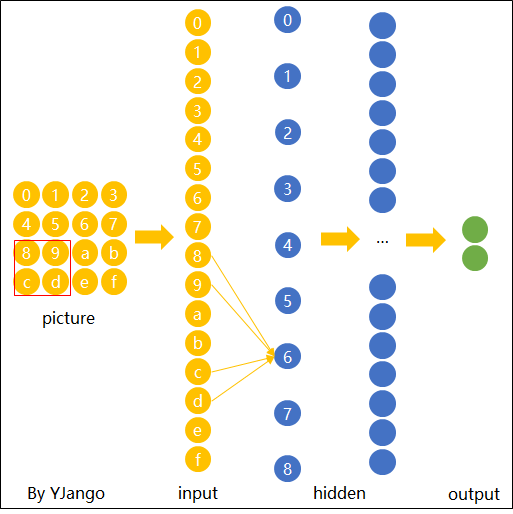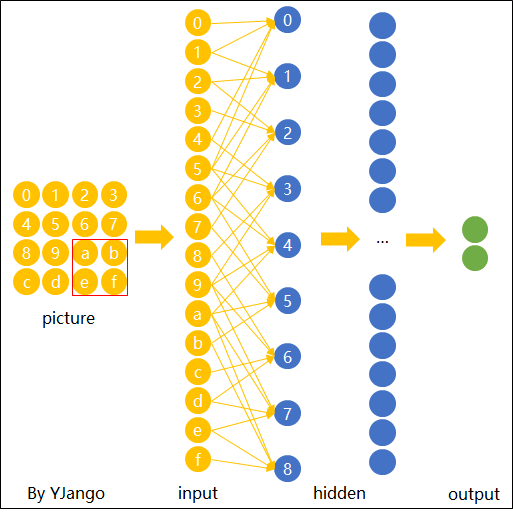
未展开形式:
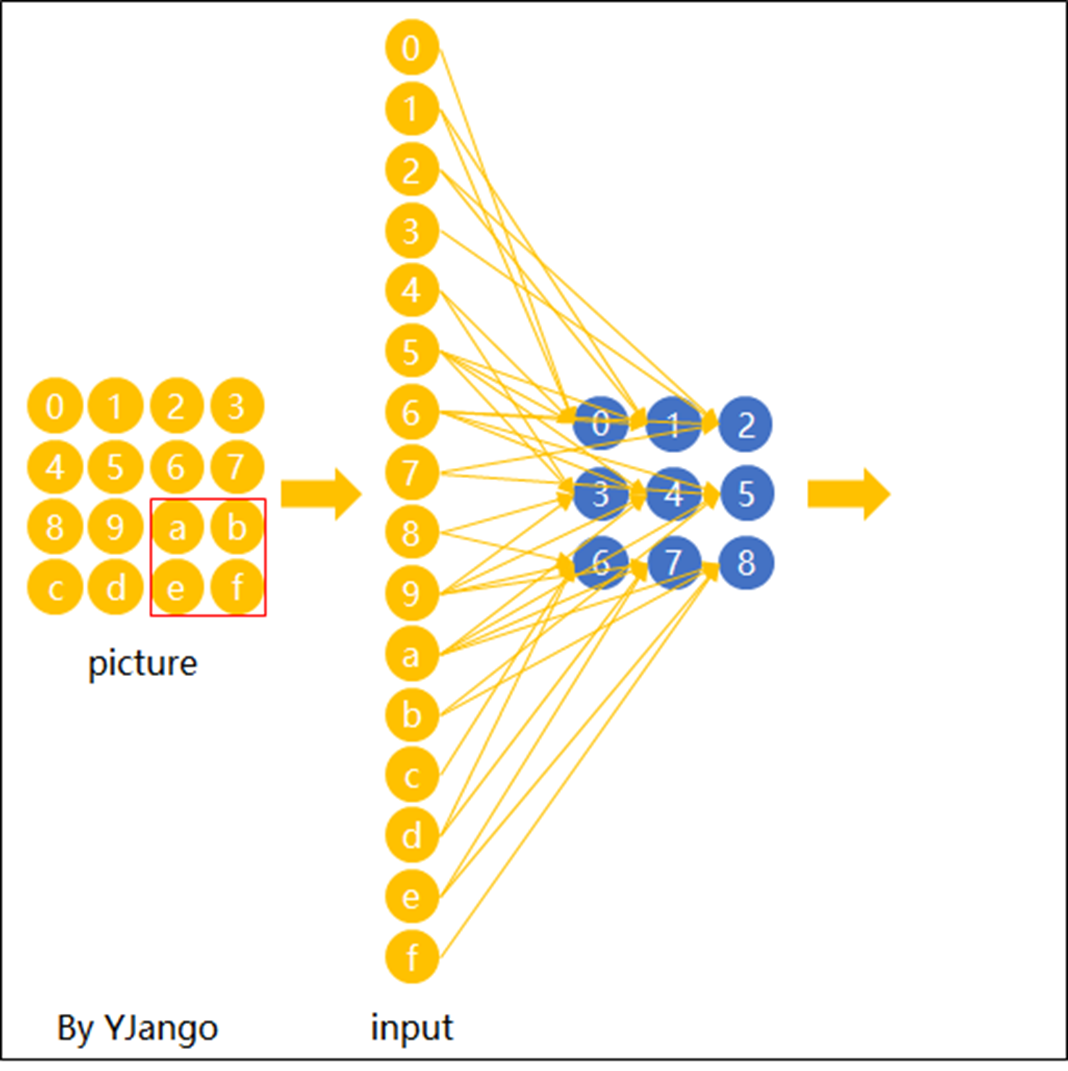
3.Application: Playing GO
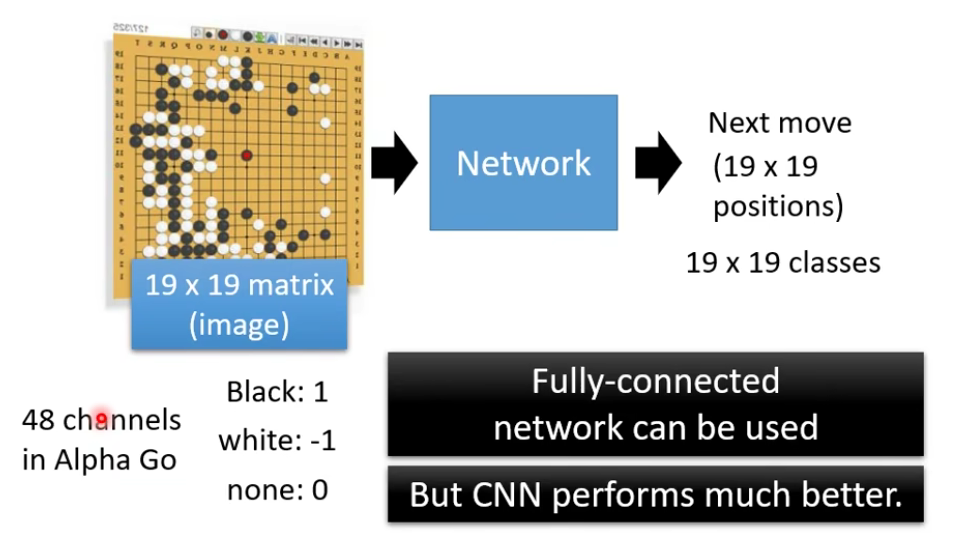
我们说CNN用在图片和影像比较好,用在别的上面效果不一定那么好。
Why CNN for GO playing?
- Some patterns are much smaller than the whole image.
- Alpha Go uses
for first layer 
- Alpha Go uses
- The same patterns appear in different regions.

从以上的观点来看,影像和下围棋有很多共通之处。
但我们还有一个问题:
- Subsampling the pixels will not change the object.
Pooling
问题是,棋局那么复杂的东西,拿掉一个row或者拿掉一colum还会没有问题吗?
How to explain this???

4. To Learn more
- CNN is not invariant to scaling and rotation(we need data augmentation(数据增强)).
data augmentation: 点击查看更多
数据增强也叫数据扩增,意思是在不实质性的增加数据的情况下,让有限的数据产生等价于更多数据的价值

比如上图,第1列是原图,后面3列是对第1列作一些随机的裁剪、旋转操作得来。
每张图对于网络来说都是不同的输入,加上原图就将数据扩充到原来的10倍。假如我们输入网络的图片的分辨率大小是256×256,若采用随机裁剪成224×224的方式,那么一张图最多可以产生32×32张不同的图,数据量扩充将近1000倍。虽然许多的图相似度太高,实际的效果并不等价,但仅仅是这样简单的一个操作,效果已经非凡了。
如果再辅助其他的数据增强方法,将获得更好的多样性,这就是数据增强的本质

进行这样一个放大或者旋转,CNN可能就不认识了。
CNN不好处理这个问题,那么有没有好的架构可以处理呢?
- Spatial Tramsformer Layer
To be continue…
- Title: 【从零开始的机器学习之旅】06-Convolutional Neural Network(CNN)
- Author: Nannan
- Created at : 2024-07-01 18:30:12
- Updated at : 2024-09-29 23:21:12
- Link: https://redefine.ohevan.com/2024/07/01/06-Convolutional Neural Network(CNN)/
- License: This work is licensed under CC BY-NC-SA 4.0.
