【从零开始的机器学习之旅】08-Self-attention

Nannan Lv5
  2024-07-02 22:30 2024-07-02 22:30 Created   2024-09-29 23:21:32 2024-09-29 23:21:32 Updated      

从零开始的机器学习之旅

-Self-attention

1. Introduction

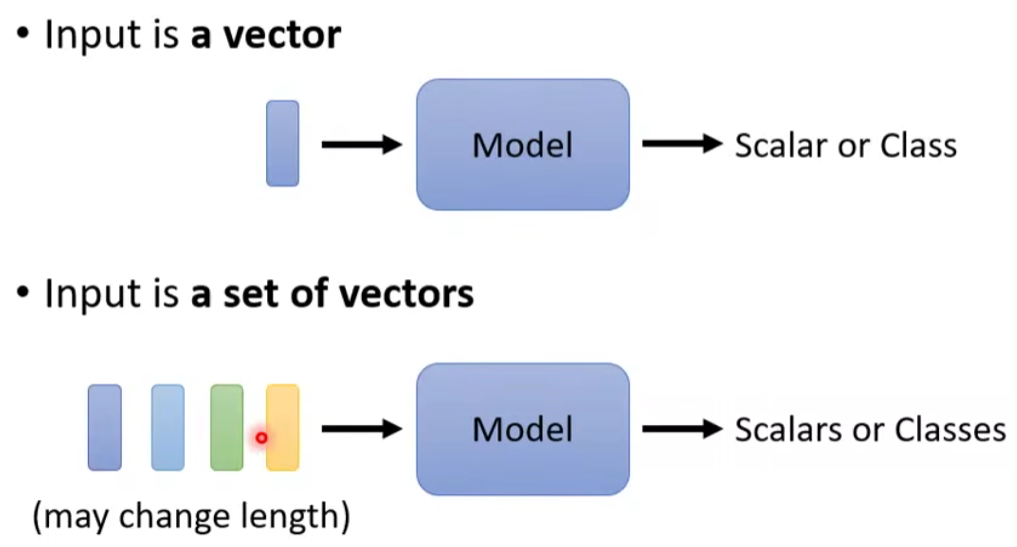
到目前为止，我们的输入都是一个向量，输出可能是一个数值或是一个类别。

假设我们遇到更复杂的问题呢？我们的输入是一排向量(Vector Set)，而且输入的向量数目是会改变的呢？这种情况应该怎么办呢？

image-20240701223218659

有什么例子是以上这种情况呢？

1.1 Vector Set as Input

加入现在我们要输入的是一个句子。那么如何把一个句子变成向量呢？

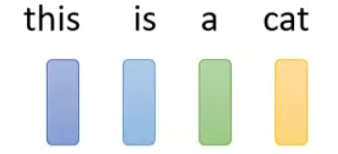
image-20240701223706447
  • One-hot Encoding
image-20240701223559789

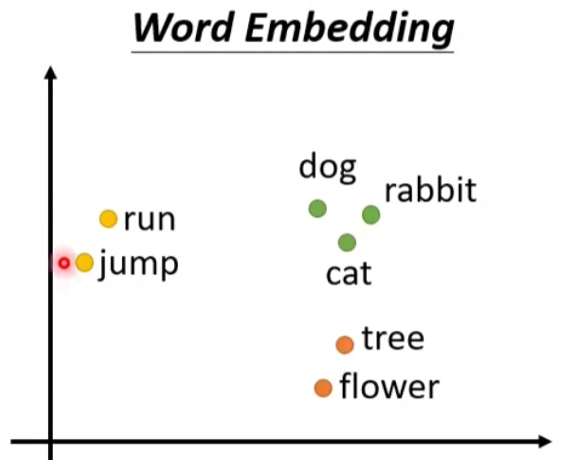
但是这种方法的缺点是我们不能知道任意两个向量之间的relation

  • Word Embedding image-20240701223652334

每个时间窗口（Window, 25ms）视为帧（Frame）,视为向量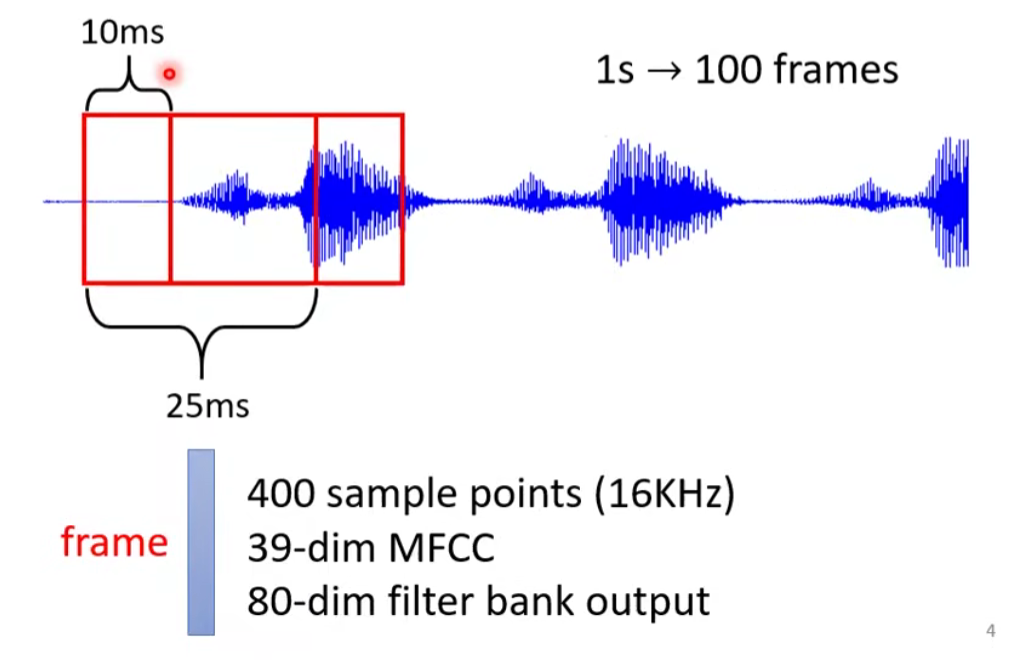image-20240701224015526

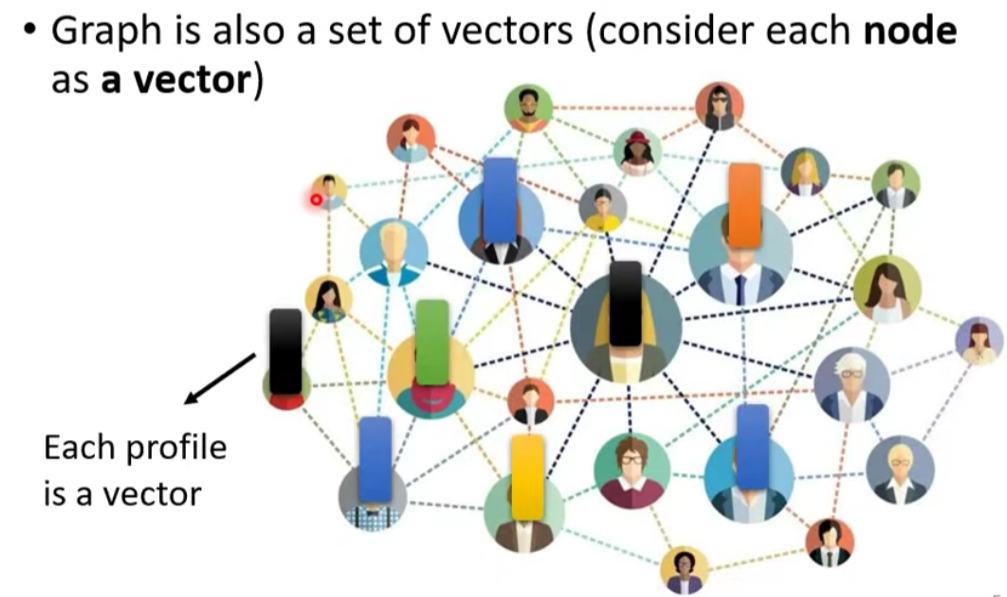
每一个节点视为一个向量

  • Social graph
image-20240701224530282
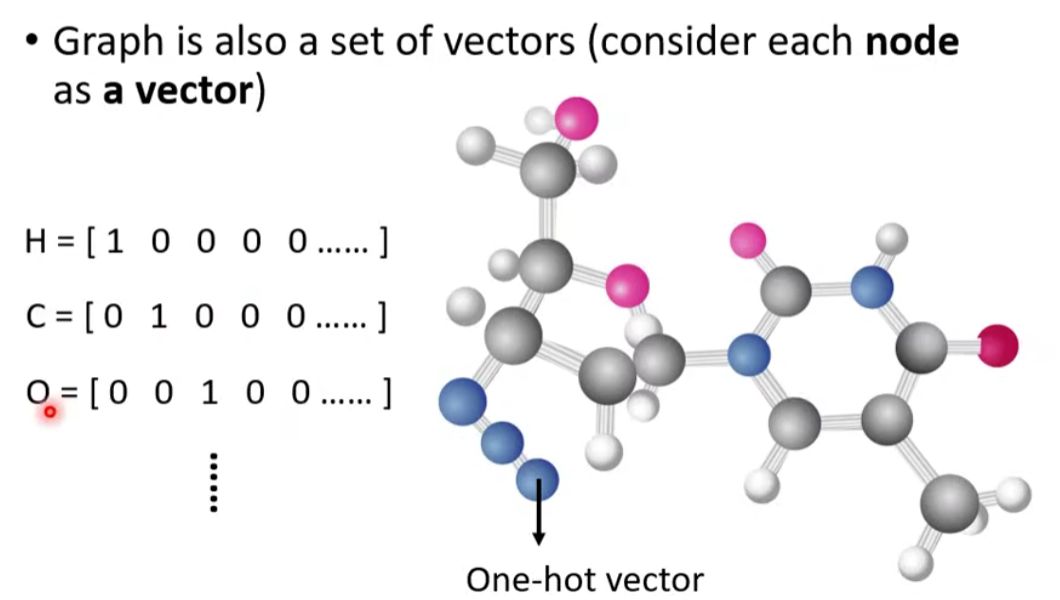
  • 分子式
image-20240701224608435

1.2 What is the output?

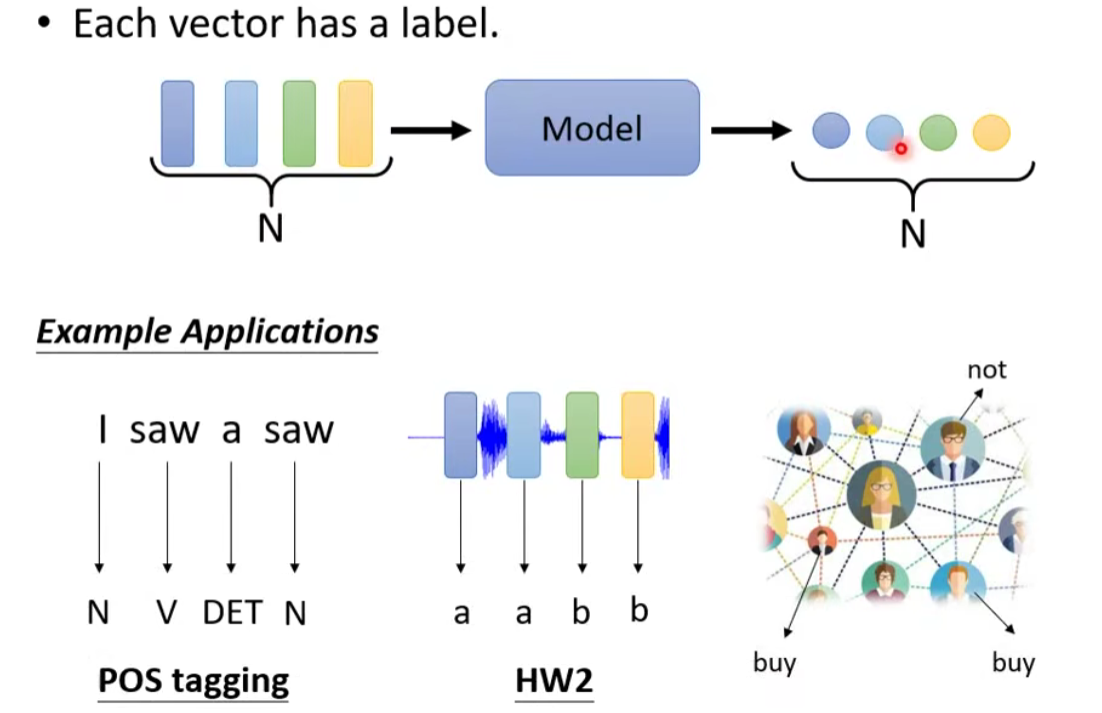
1.2.1 ( focus of this lecture⭐)输入输出数量相等【每一个向量都有一个标签】 Sequence Labeling

  • 词性标注(POS tagging)
  • 语音辨识(每一个vector对应phoneme)
  • 社交网络(每个节点(人)进行标注【是否推送商品】)
image-20240701225549135

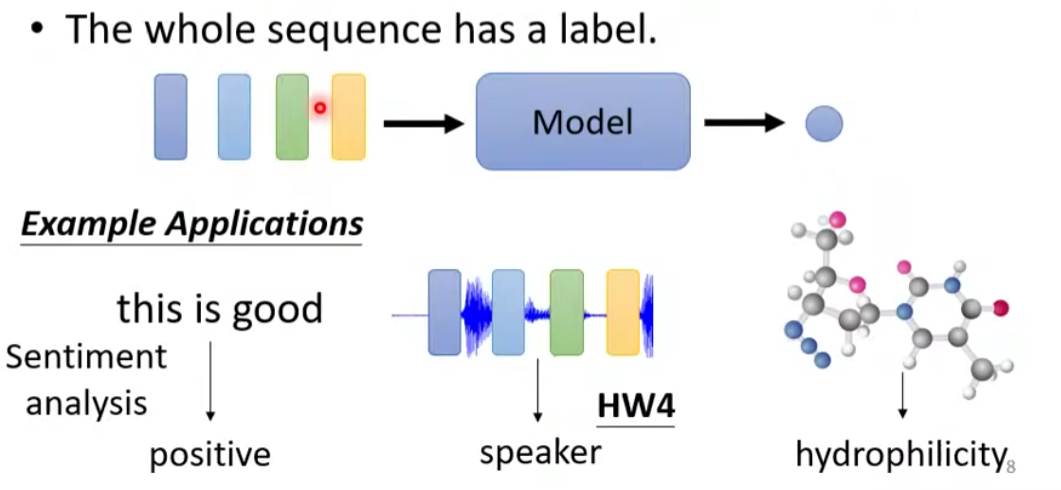
1.2.2 整个输入序列只有一个输出

  • 文本情感分析
  • 语者辨认
  • 分子的疏水性
image-20240701225749525

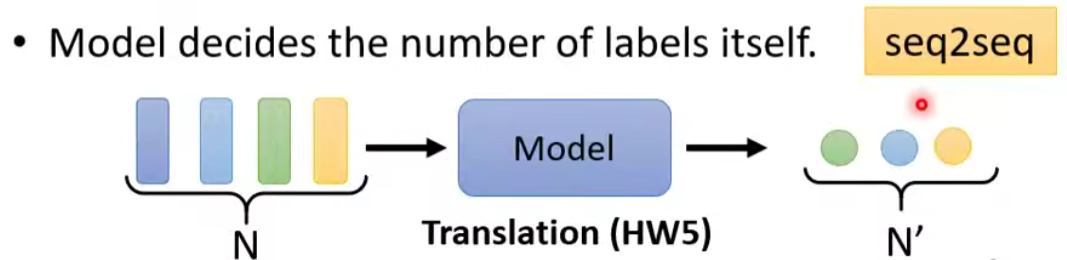
1.2.4 由模型决定输出的数目【seq2seq】

  • 翻译
  • 语音辨识
image-20240701225837404

2. Sequence Labeling

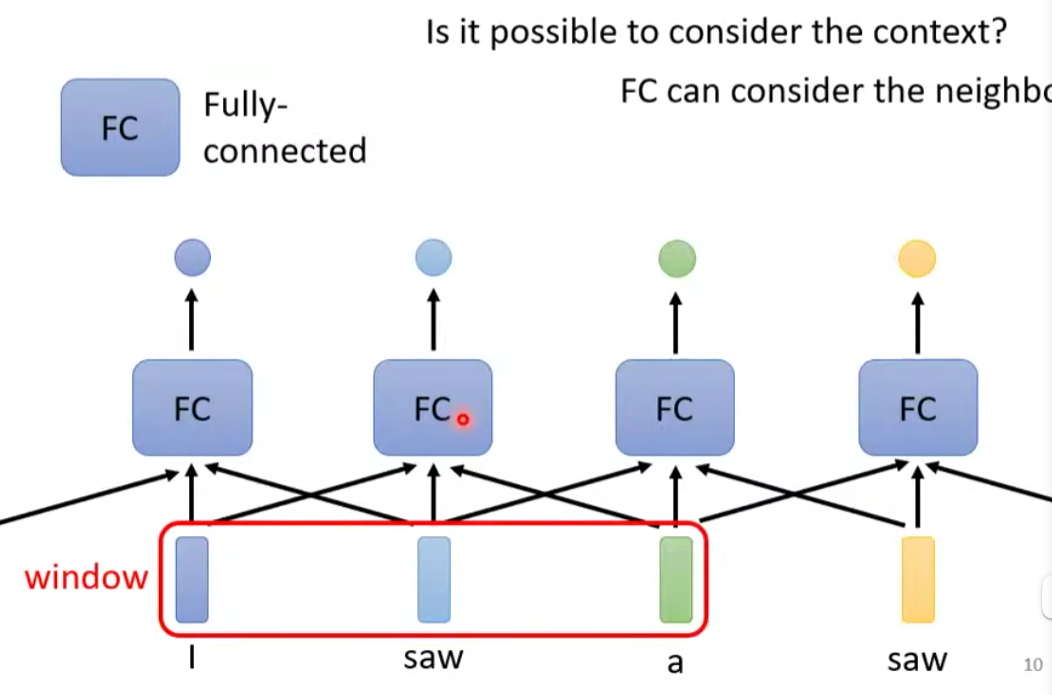
image-20240701230445980

给FC一个window的咨询，让它可以考虑上下文的。

问题是，现在如果不是考虑一个window就能解决的，而是要考虑整个sequence的情况怎么办呢？

How to consider the whole sequence?A window covers the whole sequence?

这样是太不行的，第一个因为今天我们的输入的sequence是有长有短的，第二个是如果开到那么大，那么FC需要很多的参数。

那么有没有更好的办法呢？—— Self-attention

3. Self-attention

3.1 特点

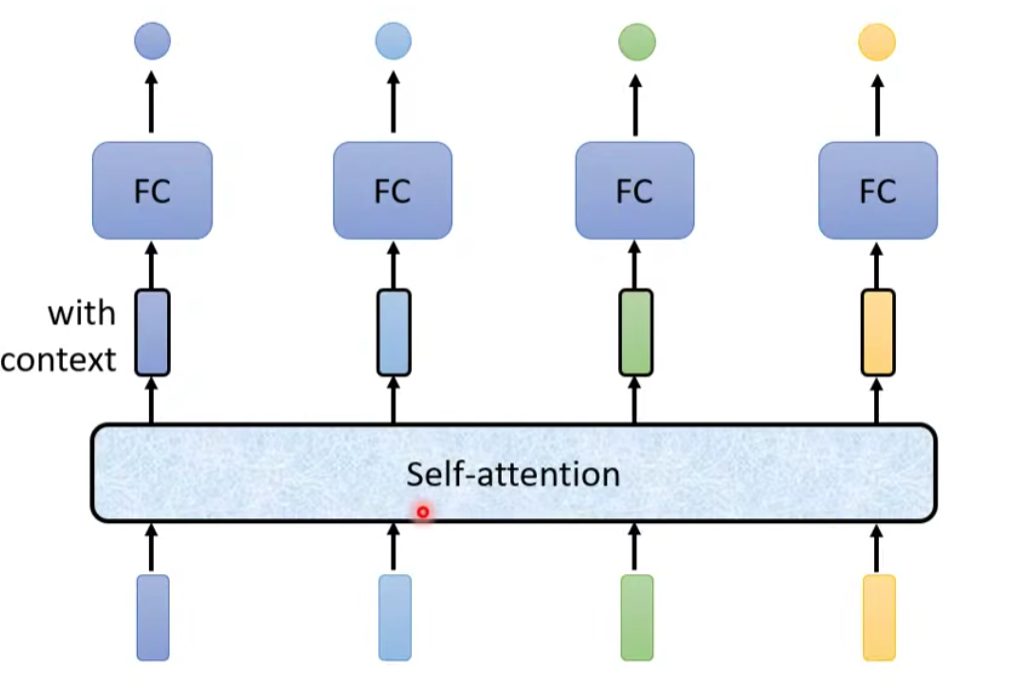
image-20240701231107146

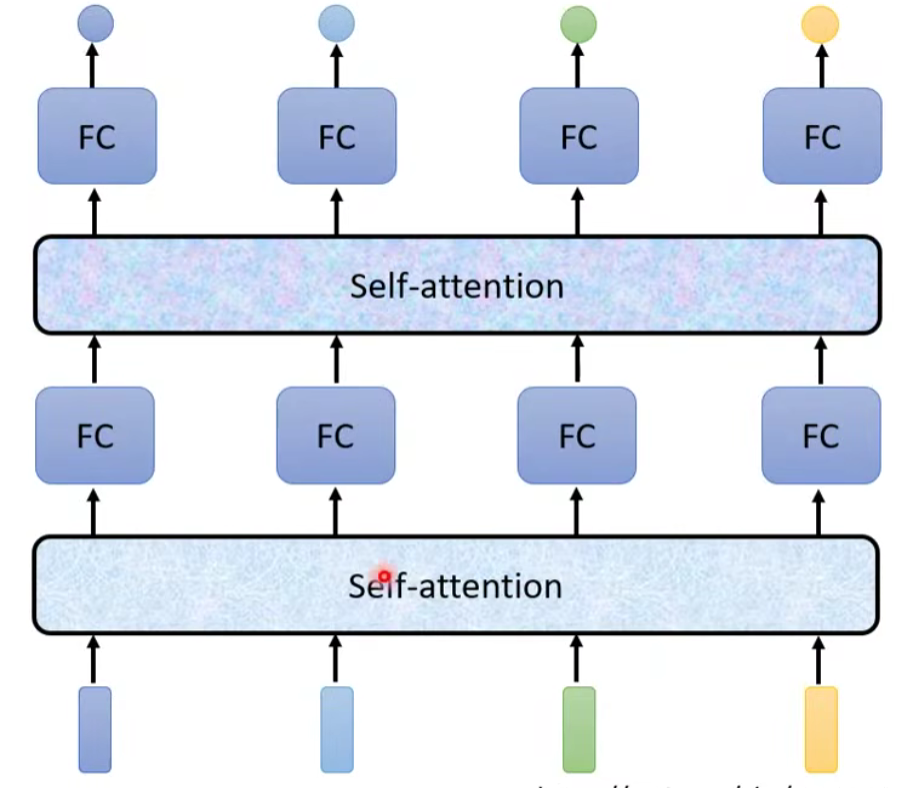
输出对每一个向量处理后的带黑框的向量(考虑整个序列 sequence 和单个向量个体的信息）。将这些向量再连接一个 FC 全连接层，输出标签，得到对应结果。

其中，self-attention 的功能是处理整个 sequence 的信息，而 FC 则是处理某一个位置的信息，Self-attention + FC 可以交替使用，知名文章：Attention is all you need ⇒Transformer。

image-20240701231323660

3.2 基本原理

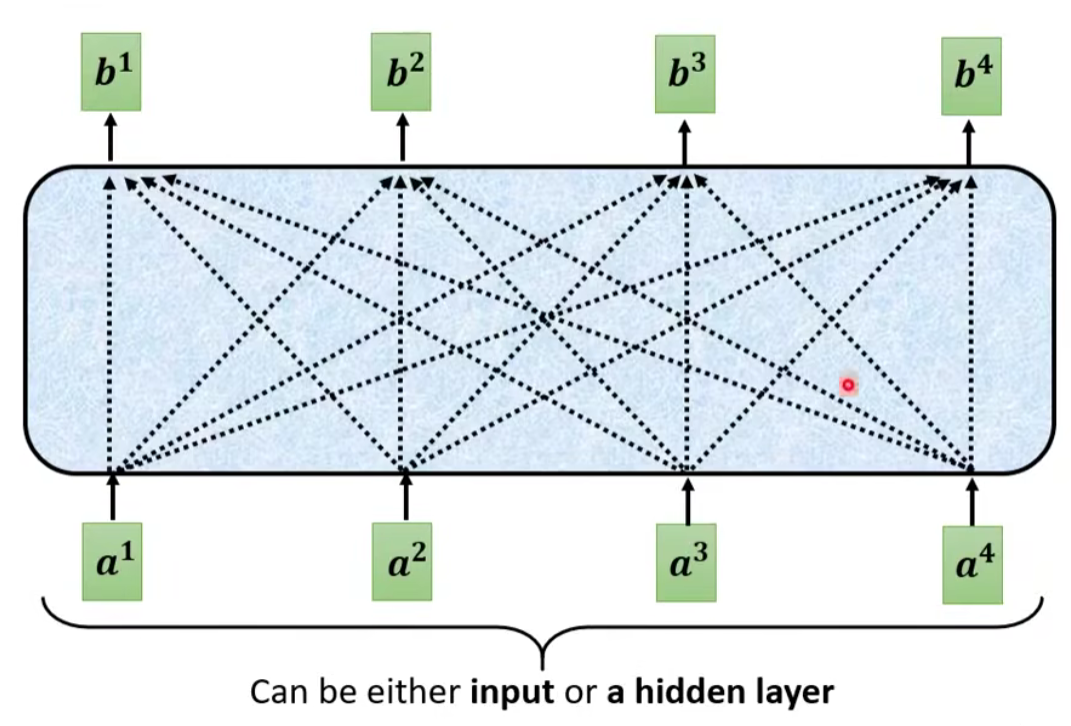
image-20240701231623401

输入：一串的 Vector，这个 Vector 可能是整个 Network 的 Input，也可能是某个 Hidden Layer 的 Output

输出：处理 Input 以后，每一个 都是考虑了所有的 以后才生成出来的

那么是如何产生的呢？

具体步骤：

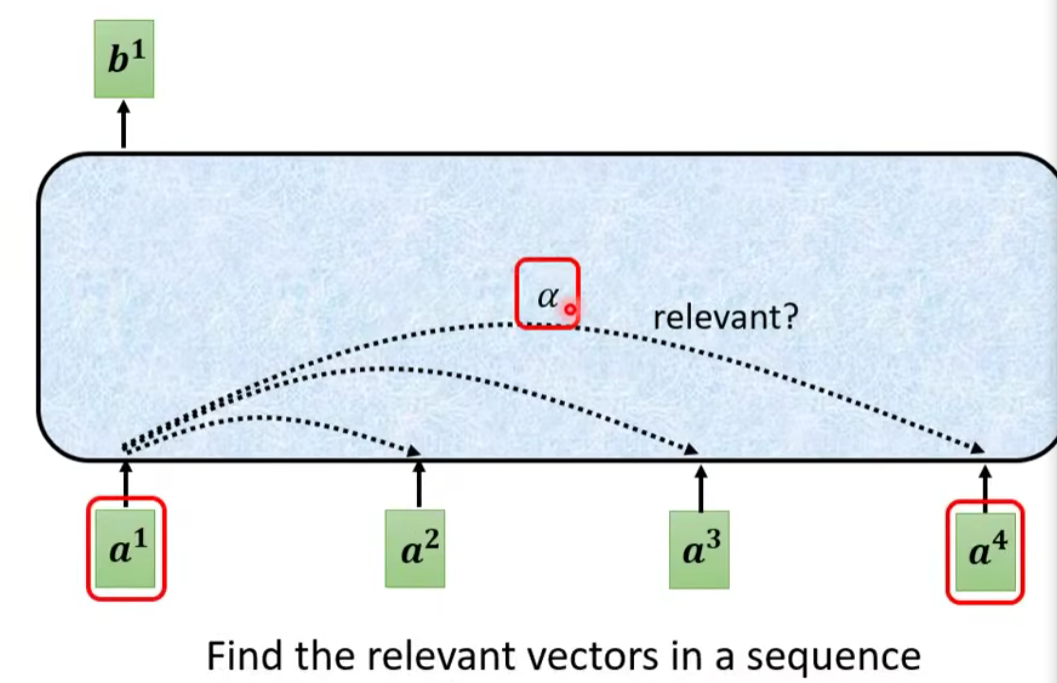
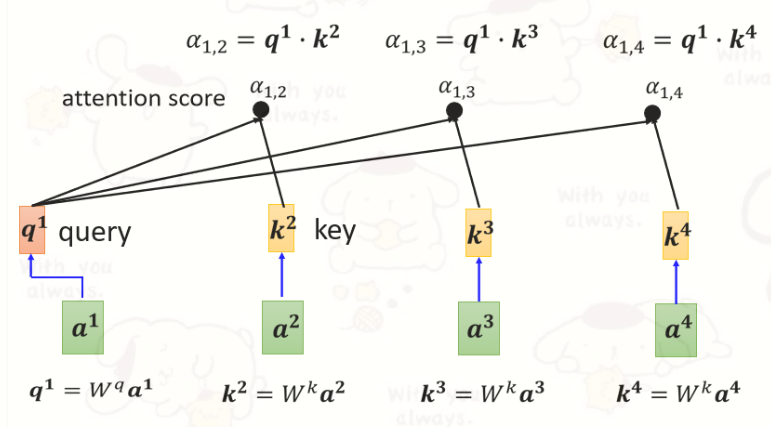
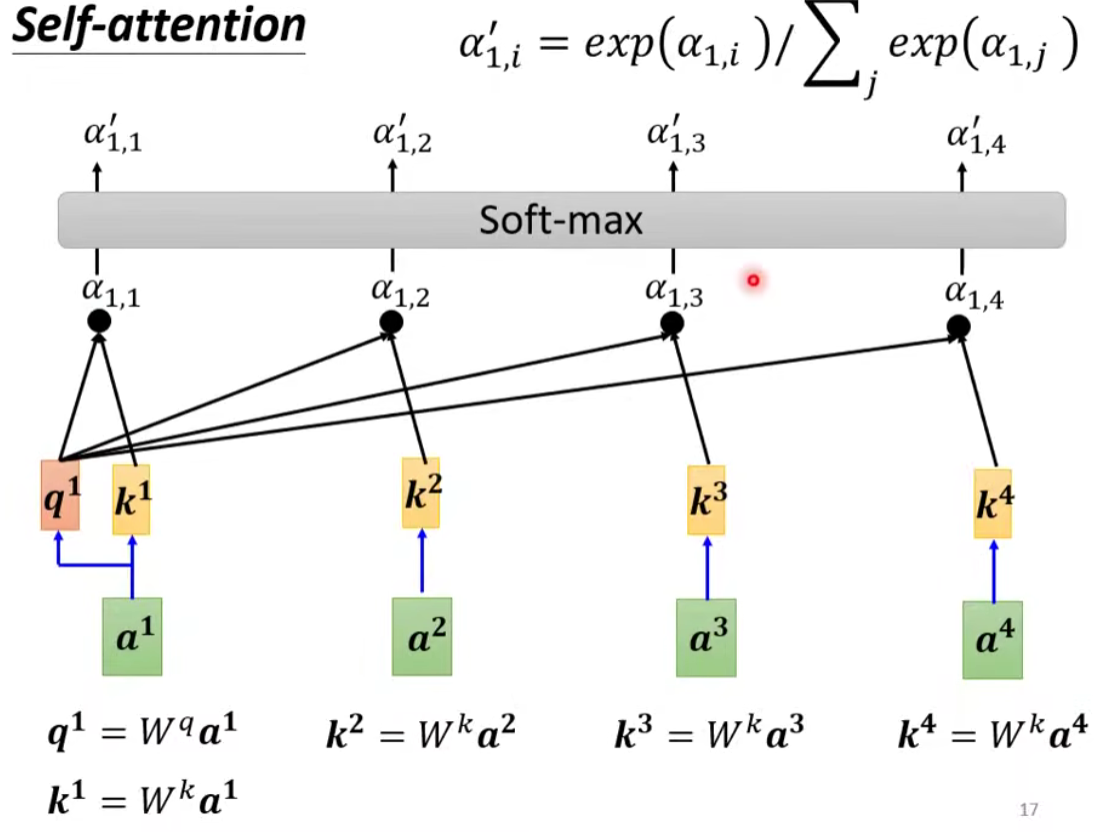
  1. 以 为例，根据 这个向量，找出整个 sequence 中跟 相关的其他向量 ⇒ 计算哪些部分是重要的，求出 和 的相关性（影响程度大的就多考虑点资讯），用 α 表示

    image-20240701232316577

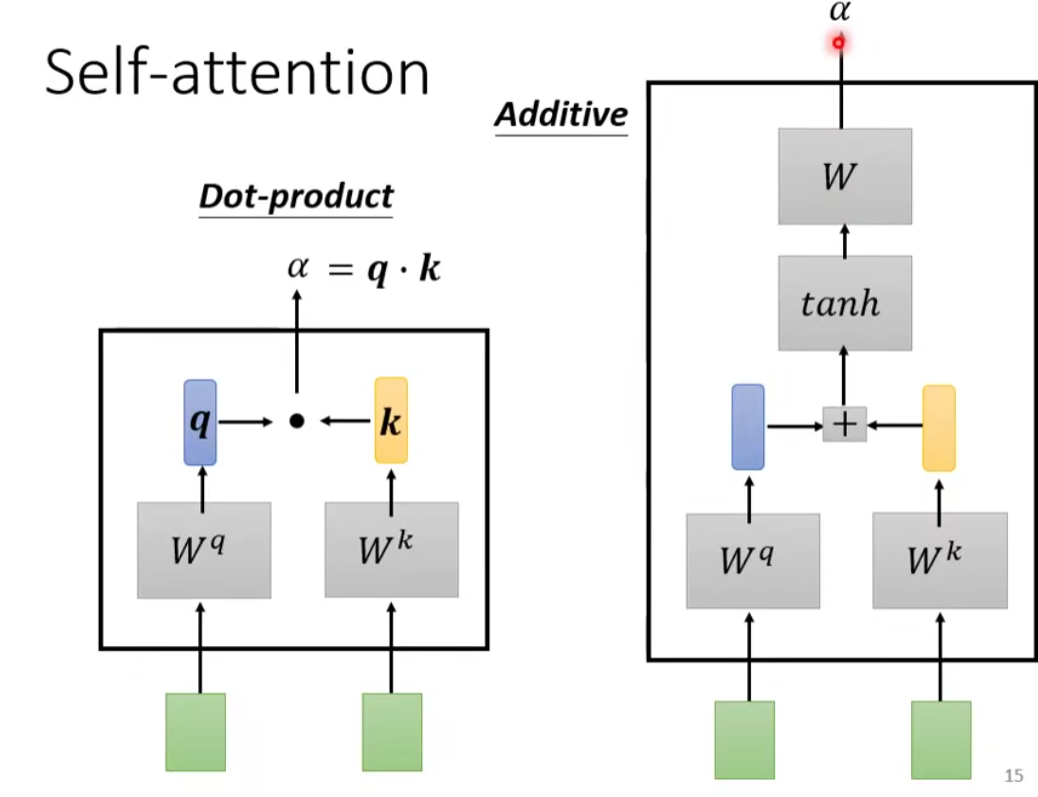
  2. 计算相关性：有 点积(Dot-product) 和 Additive 两种方法计算相关性，我们主要讨论 点积 这个方法。输入的两个向量分别乘不同的矩阵，左边这个向量乘上矩阵 得到矩阵 （query），右边这个向量乘上矩阵 得到矩阵（key），再把 q 跟 做 dot product（点积），逐元素相乘后累加得到一个 scalar 就是 相关性 α

怎么产生

image-20240701232523331

怎么把它套用在self-attention里面呢？

把 乘上 得到 ，叫做 Query（就像是搜寻相关文章的关键字，所以叫做 Query）

然后将 都要乘 得到 ，叫做 Key，把这个Query 和 Key 进行 点积操作 就得到 相关性 α（ α 叫做 Attention Score，表示 Attention计算出的 vector 之间的相关性）

image-20240701232736138

一般我们还要和自己做关联性。attention score 还要经过一层 softmax 才能用于后续处理，其中 softmax 也可以换成其他的 activation function。

image-20240701233905462
  1. 分别抽取重要信息，根据关联性作加权求和得到 （一次性并行计算出 ，不需要依次先后得出。

做法：

  • 首先把到这边每一个向量都乘上得到新的向量用表示
  • 接下来把到每一个向量都乘上Attention score
  • 然后再把它们加起来得到
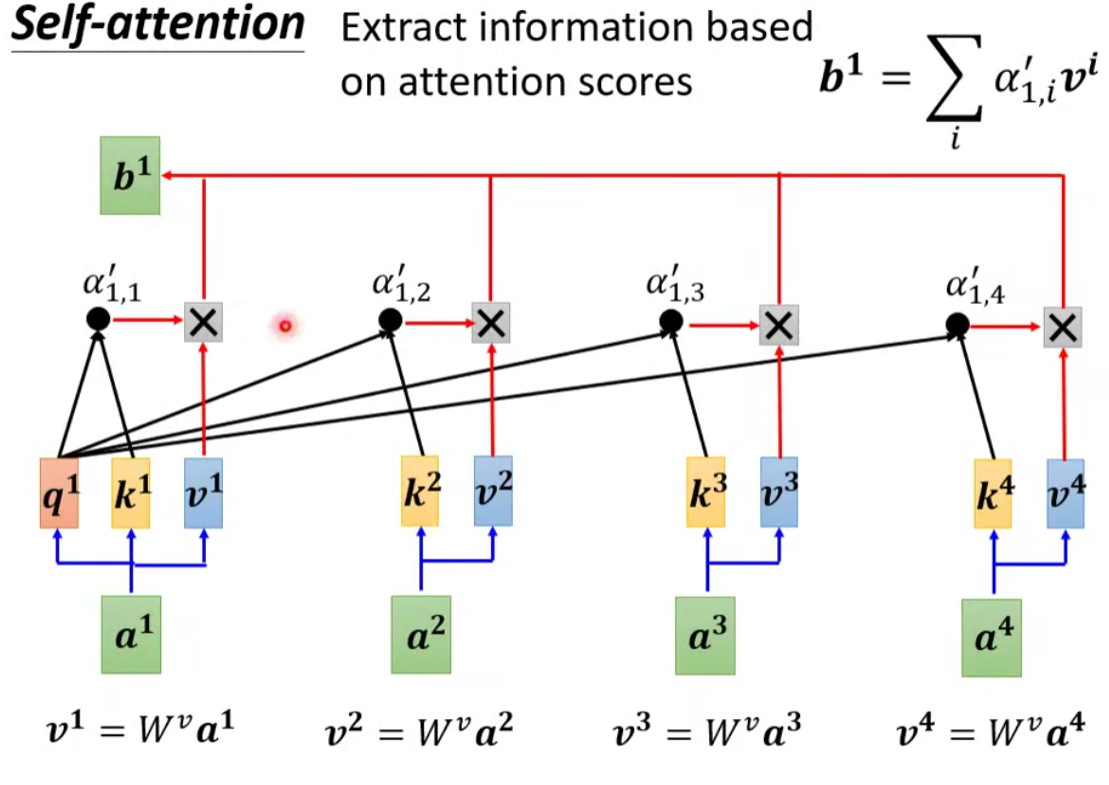
image-20240702000057712

如果某一个向量它得到的分数越高，比如说和的关联性很强，这个得到的值很大，那我们今天做完Weighted Sum之后得到的就可能会比较接近

总而言之：谁的Attention score 的分数最大，谁的那个就会Dominant你抽出来的结果。

注意：我们的到并不需要按顺序一次产生，它们是一次性产生的。

3.3 从矩阵乘法的角度分析运作过程

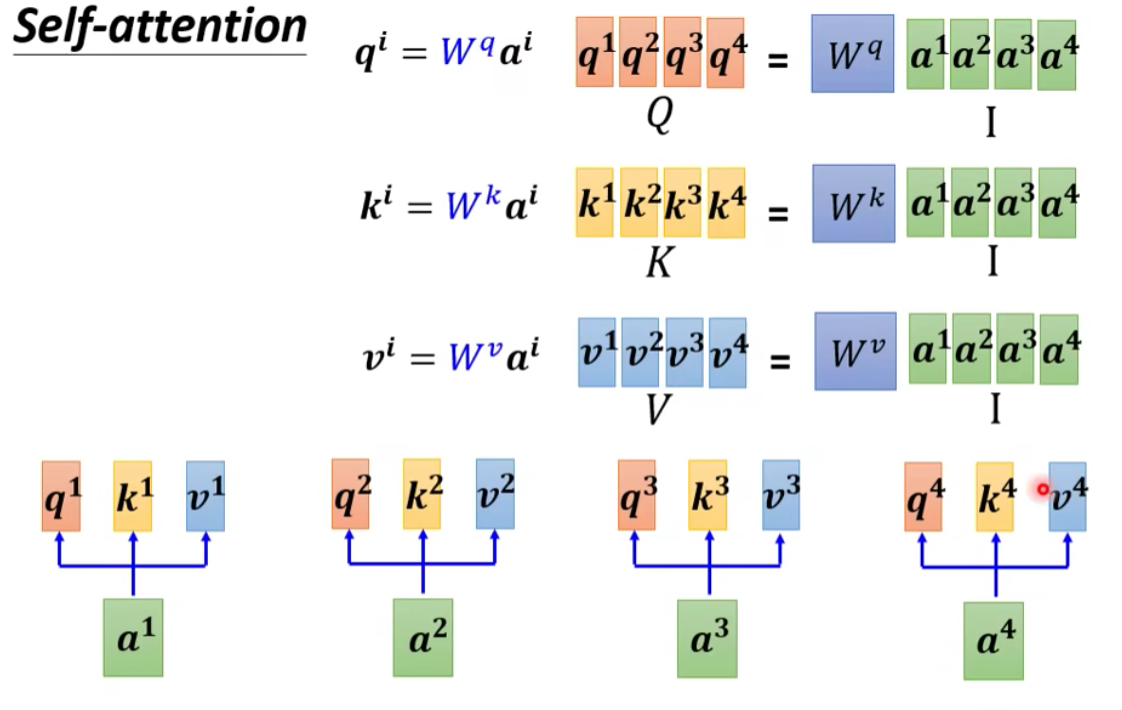
① 从 得到 （其中 、 和 都是要学习的网络参数矩阵）

image-20240702001736777

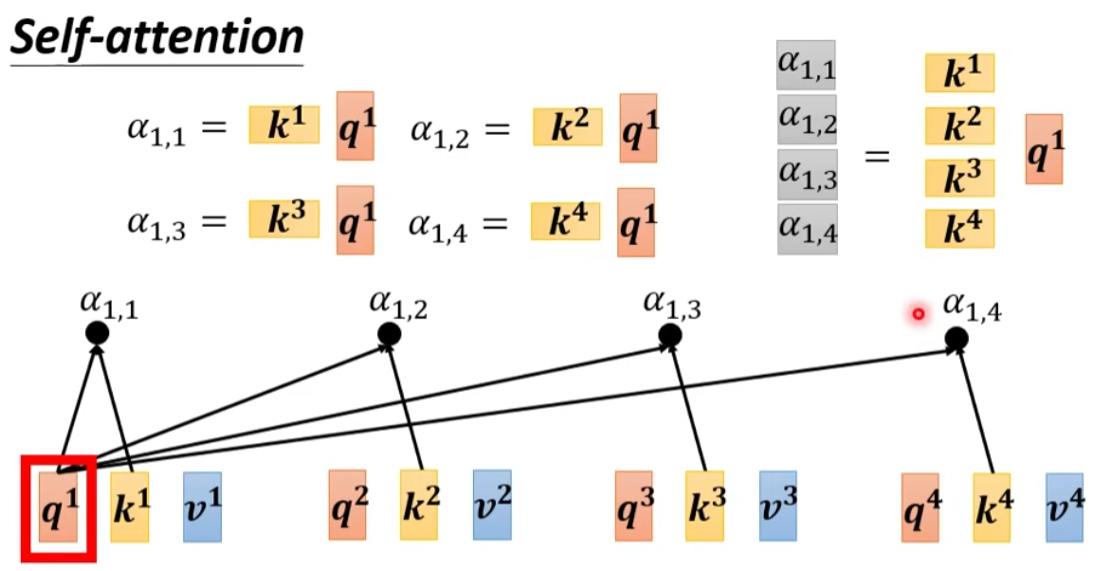
② 计算 α 并 Normalization

image-20240702002010023

其他几个和同理：

image-20240702002158565

③ 计算 b

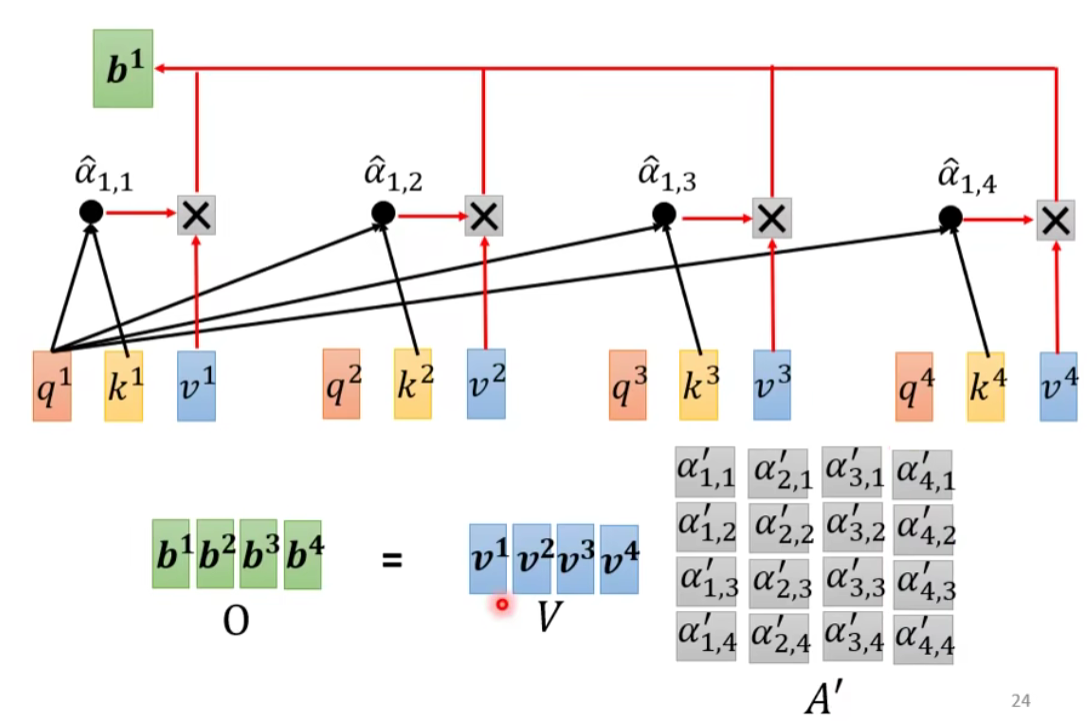
image-20240702002403310

简而言之就是以下操作：

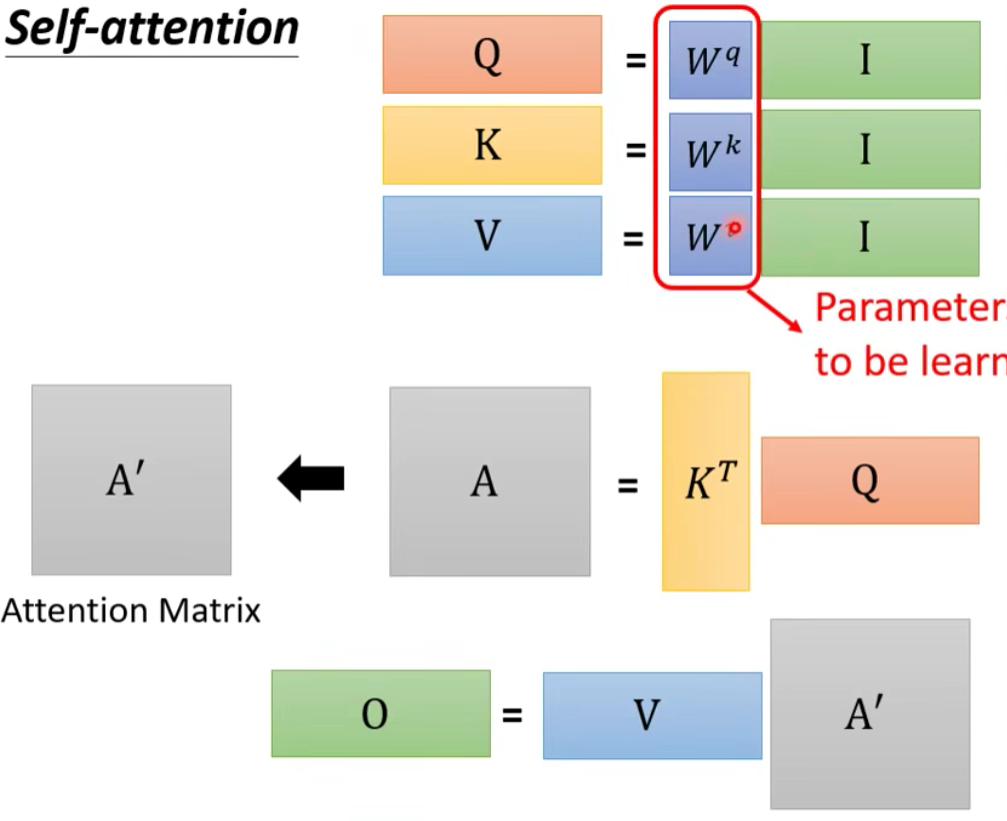
image-20240702002621328

其中：

  • I 是 Self-attention 的 input（一排 vector），每个 vector 拼起来当作矩阵的 column
  • 这个 input 分别乘上三个矩阵， 得到 Q K V
  • 接下来 Q 乘上 K 的 transpose,得到 A 。可能会做一些处理,得到 A’ ,叫做Attention Matrix ，生成 Q 矩阵就是为了得到 Attention 的 score
  • A’ 再乘上 V，就得到 O，O 就是 Self-attention 这个 layer 的输出

4. Multi-head Self-attention(Different types of relevance)

4.1 特点

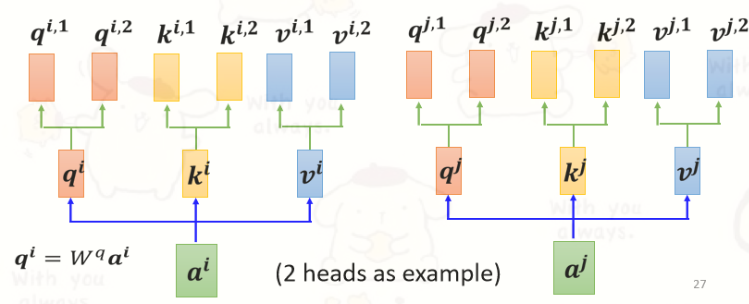
使用多个组合，不同的负责不同种类的相关性。

例如在下图中，一共有2类， 1类的放在一起算，2类的放在一起算。相关性变多了，所以参数也增加了，原来只需要三个 W 矩阵，现在需要六个 W 矩阵。

image-20240702120603517

4.2 计算步骤

  • 先把 乘上一个矩阵得到 。
  • 再把 乘上另外两个矩阵，分别得到 跟 ，代表有两个 head；同理可以得到 ，，， 。
  • 同一个head里的 计算 。

下面我们来看看两个head的例子：

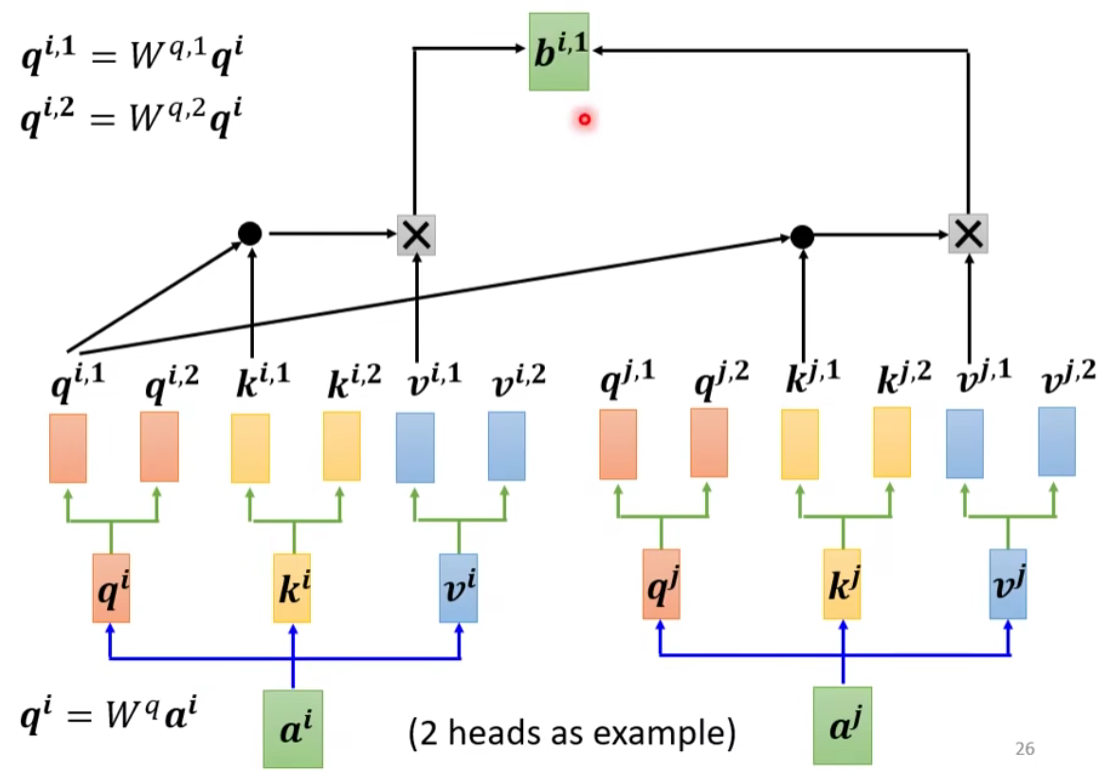
image-20240702120335080

同理对第二组也是一样的操作：

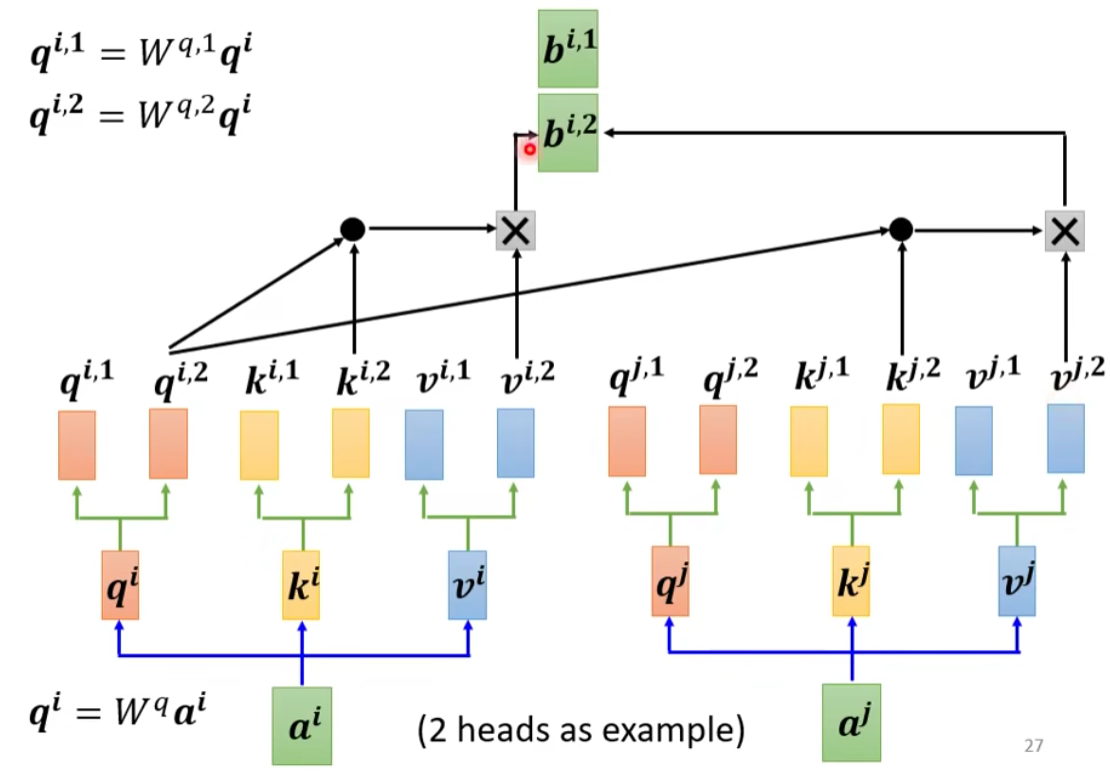
image-20240702120410459

然后将各个 head 计算得到的 拼接，通过一个 transform得到 ，再送到下一层去：image-20240702120519104

5.Positional Encoding

  • No position information in self-attention.

在前面的讲解中我们发现，都没有位置咨询。

那么我们应该怎么把位置的咨询加进去呢？

  • Each position has a unique positional vector

方法：每个位置用一个 vector ei 来表示它是 sequence 的第 i 个。加和到原向量中。

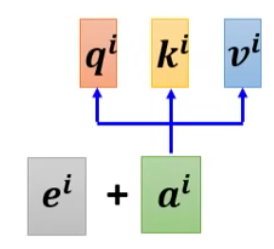
image-20240702122742041

这些位置咨询可以hand-crafted 也可以 learned form data

5.1 why need Positional Encoding?

优点：

  1. 解决了长序列依赖问题
  2. 可以并行

缺点：

  1. 开销变大了
  2. 既然可以并行，也就是说，词与词之间不存在顺序关系（打乱一句话，这句话里的每个词的词向量依然不会变），即无位置关系（既然没有，我就加一个，通过位置编码的形式加）

6. Self-addtention 的应用

  1. NLP
image-20240702123353286
  1. Speech
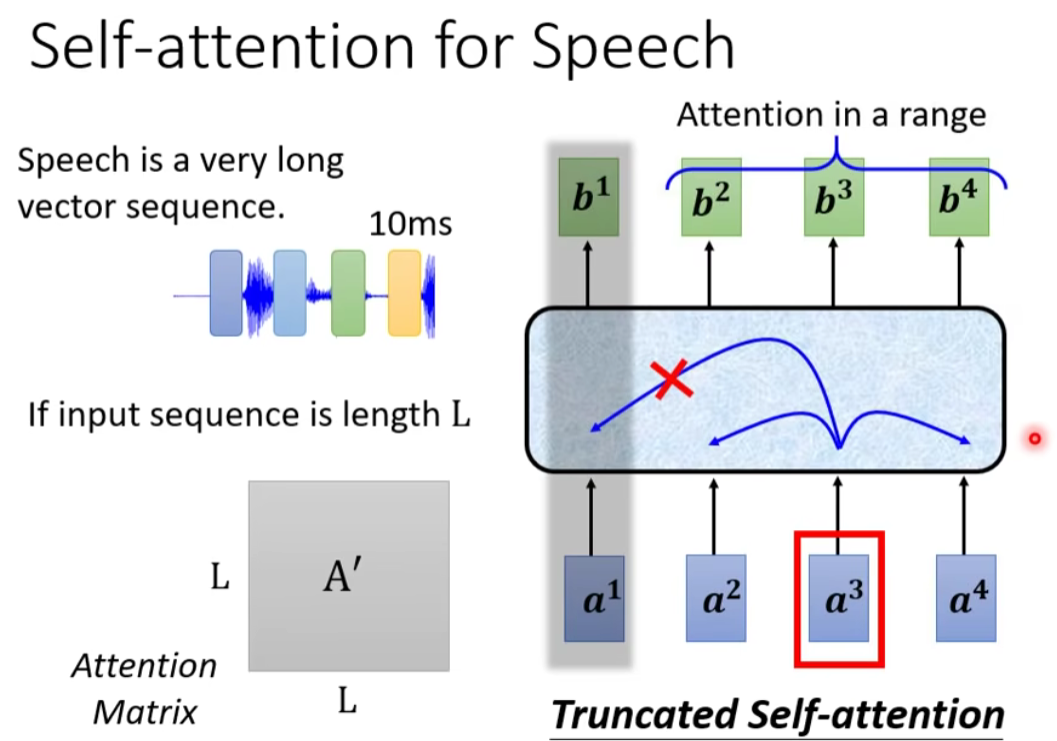
image-20240702123619854
  1. Image
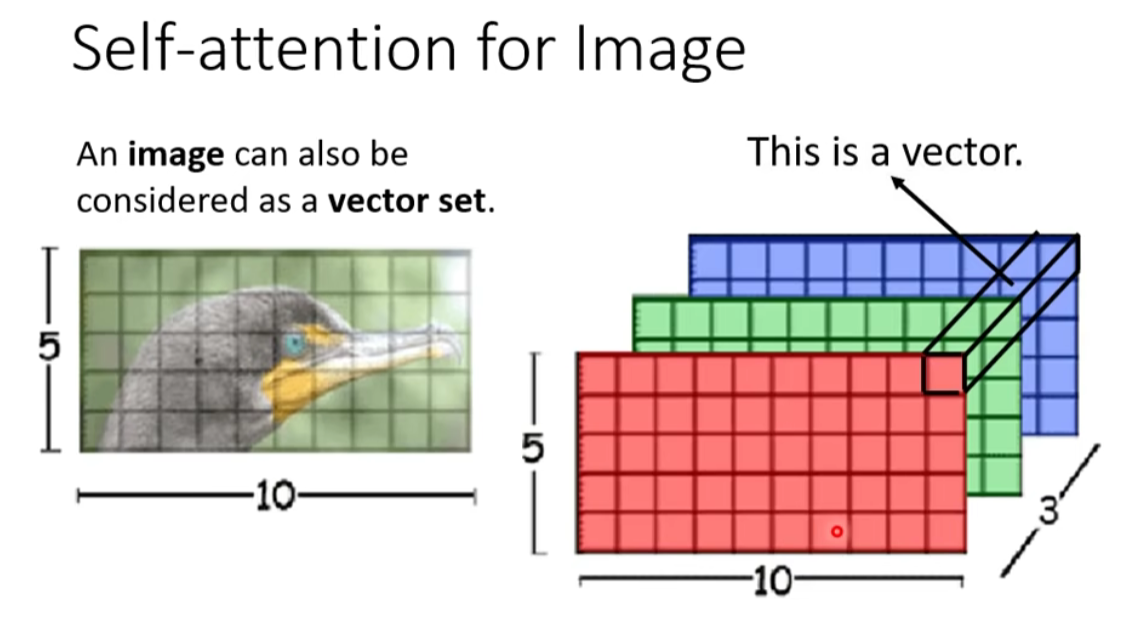
image-20240702123735044
  1. Graph
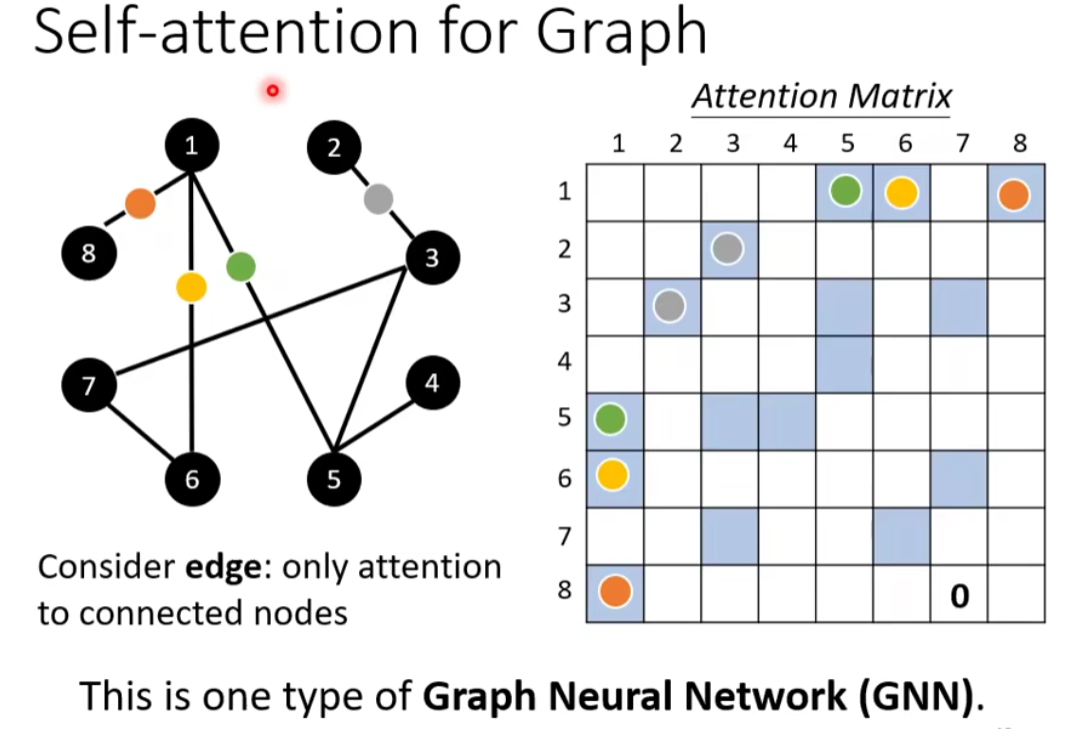
image-20240702130436605
  • 在 Graph 上面，每一个 node 可以表示成一个向量
  • node 之间是有相连的，每一个 edge 标志着 node 跟 node 之间的关联性
  • 比如：在做Attention Matrix 计算的时候，只需计算有 edge 相连的 node
  • 因為这个 Graph 往往是人为根据某些 domain knowledge 建出来的，已知这两个向量彼此之间没有关联（图矩阵中对应结点 i 与 结点 j 之间没有数值），就没有必要再用机器去学习这件事情

7.Self-attention v.s. CNN

CNN 可以看成简化版的 self-attention，CNN 就是只计算感受野中的相关性的self-attention。

或者你可以说self-attention是一个复杂化的CNN，self-attention就是CNN有着可学习的感受野。

  • CNN：感知域（receptive field）是人为设定的，只考虑范围内的信息
  • Self-attention：考虑一个像素和整张图片的信息 ⇒ 自己学出“感知域”的形状和大小

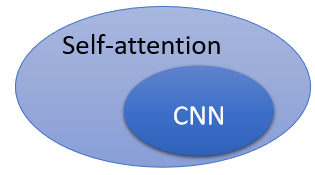
conclusion：

结论：

CNN 就是 Self-attention 的特例，Self-attention 只要设定合适的参数，就可以做到跟 CNN 一模一样的事情。

img

self attention 是更 flexible 的 CNN

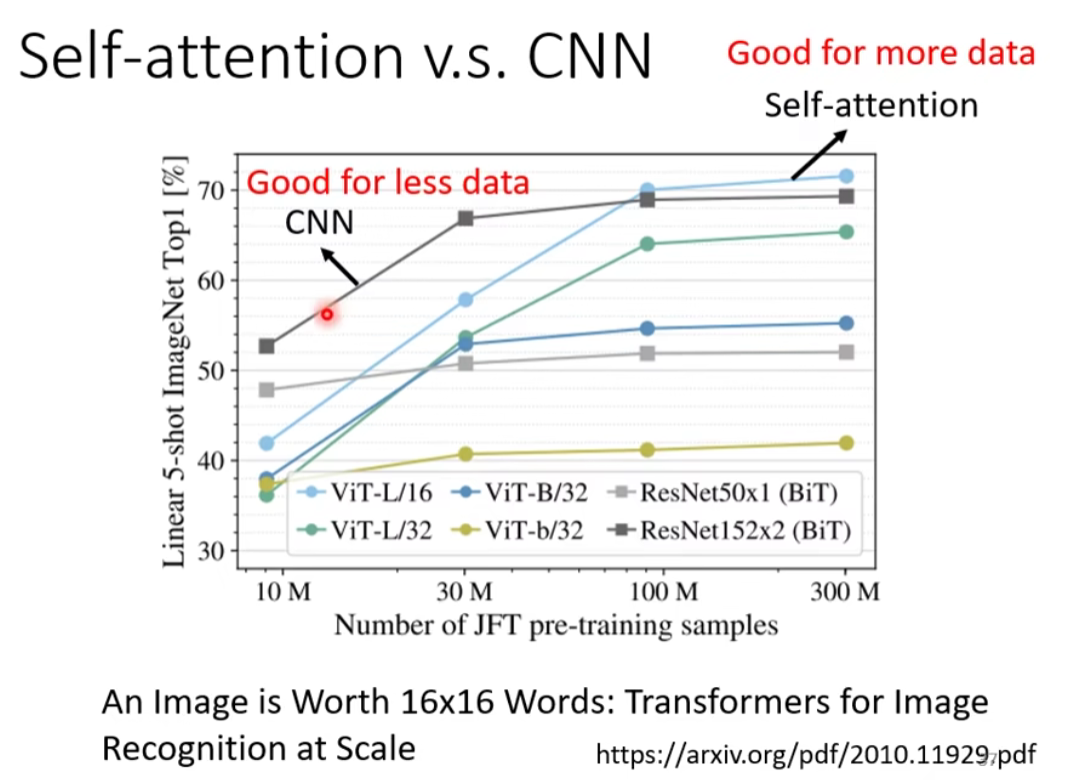
⇒ 比较flexible的model(self-attention) 需要 更多的数据 进行训练，否则会 欠拟合；否则CNN的性能更好

  • Self-attention 它弹性比较大,所以需要比较多的训练资料,训练资料少的时候,就会 overfitting
  • 而 CNN 它弹性比较小,在训练资料少的时候,结果比较好,但训练资料多的时候,它没有办法从更大量的训练资料得到好处
image-20240702125510811

8.Self-attention v.s. RNN

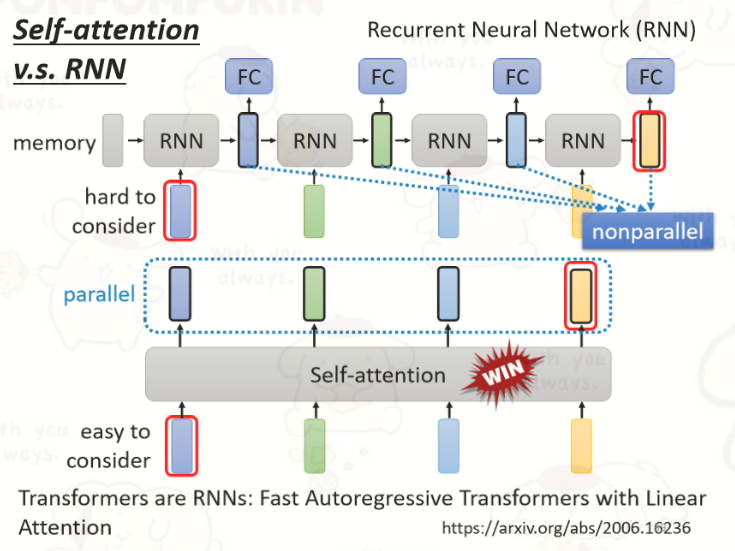
image-20240702125940883
  • 对 RNN 来说，最终的输出要考虑最左边一开始的输入 vector，意味着必须要把最左边的输入存到 memory 里面并且在计算过程中一直都不能够忘掉，一路带到最右边，才能够在最后一个时间点被考虑（依次按顺序输出）
  • 对 Self-attention 可以在整个 sequence 上非常远的 vector之间轻易地抽取信息（并行输出，速度更快，效率更高）
  • Title: 【从零开始的机器学习之旅】08-Self-attention
  • Author: Nannan
  • Created at : 2024-07-02 22:30:00
  • Updated at : 2024-09-29 23:21:32
  • Link: https://redefine.ohevan.com/2024/07/02/08-self-attention/
  • License: This work is licensed under CC BY-NC-SA 4.0.
Comments
On this page
【从零开始的机器学习之旅】08-Self-attention
  1. 从零开始的机器学习之旅
  2. -Self-attention
    1. 1. Introduction
      1. 1.1 Vector Set as Input
      2. 1.2 What is the output?
        1. 1.2.1 ( focus of this lecture⭐)输入输出数量相等【每一个向量都有一个标签】 Sequence Labeling
        2. 1.2.2 整个输入序列只有一个输出
        3. 1.2.4 由模型决定输出的数目【seq2seq】
    2. 2. Sequence Labeling
    3. 3. Self-attention
      1. 3.1 特点
      2. 3.2 基本原理
      3. 3.3 从矩阵乘法的角度分析运作过程
    4. 4. Multi-head Self-attention(Different types of relevance)
      1. 4.1 特点
      2. 4.2 计算步骤
    5. 5.Positional Encoding
      1. 5.1 why need Positional Encoding?
    6. 6. Self-addtention 的应用
    7. 7.Self-attention v.s. CNN
    8. 8.Self-attention v.s. RNN